系统性风险与非系统性风险
系统性风险与非系统性风险相关课程
 系统性风险与非系统性风险考点解析
系统性风险与非系统性风险考点解析
 系统性风险与非系统性风险介绍
系统性风险与非系统性风险介绍
系统性风险与非系统性风险
|
系统性风险 |
①不可分散 ②例:政策风险、利率风险、购买力风险、市场风险 |
|
|
非系统性风险 |
①可通过分散投资降低甚至消除 ②例:经营风险、财务风险、信用风险、偶然事件风险 |
|
系统性风险与非系统性风险考点试题
大咖讲解:系统性风险与非系统性风险


有效性市场理论
有效性市场理论
(1)随机漫步
随机漫步理论认为,股票价格的变动是随机且完全不可预测的。股价中包含了当前一切可以用于预测股票表现的信息。
(2)有效市场假说
有效市场假说认为,证券价格已经充分反映了所有相关的信息,资本市场相对于这个信息集是有效的,任何人根据这个信息集进行交易都无法获得经济利润。
(3)有效市场的类型
|
类型 |
股价包含的信息 |
是否可获得超额利润 |
|
弱式有效市场 |
市场交易数据如历史股价、交易量 |
技术分析无效,基本分析不确定,掌握内幕信息可能获得经济利润 |
|
半强式有效市场 |
所有公开信息如财务报表、历史价量 |
技术分析和基本分析均无效掌握内幕信息可能获得经济利润 |
|
强式有效市场 |
所有公开信息和内幕信息 |
技术分析和基本分析均无效 |

投资组合理论
投资组合理论
|
系统性风险与非系统性风险 |
系统性风险 |
①不可分散 ②例:政策风险、利率风险、购买力风险、市场风险 |
|
|
非系统性风险 |
①可通过分散投资降低甚至消除 ②例:经营风险、财务风险、信用风险、偶然事件风险 |
||
|
预期收益率 |
Ri为某一资产在第i种情形下的投资收益率; pi为投资收益率可能发生的概率。 |
||
|
必要收益率 |
必要收益率=无风险收益率+风险收益率 |
||
|
实际收益率与名义收益率 |
名义收益率=(1+实际收益率)×(1+预期通货膨胀率)-1 实际收益率=(1+名义收益率)/(1+预期通货膨胀率)-1 |
||
|
方差/标准差 |
投资组合实际收益率围绕预期收益率的波动。 预期收益率的标准差越大,预期收益率的分布越大,不确定性及风险越大。 |
||
|
协方差与相关系数 |
协方差 |
①两个随机变量协同运动的程度和方向,取值(-∞,+∞) ②协方差>0,投资组合种的两种资产的收益同向变动 ③协方差<0,投资组合种的两种资产的收益反向变动 ④协方差=0,两种金融资产的收益没有相关关系 |
|
|
相关系数ρ |
①协方差的标准化,取值范围[-1,+1] ②相关系数为正,协方差为正;ρij=1,完全正相关 ③相关系数为负,协方差为负;ρij=-1,完全负相关 ④相关系数为0,协方差为0,表明两个随机变量不相关 |
||
|
β系数 |
①度量特定资产(或资产组合)的系统性风险 ②度量一种证券或投资组合相对总体市场的波动性 ③β越大,投机性越强 |
||
|
风险溢价 |
超出无风险收益率之上的必要收益率 |
||
|
效用 |
消费者在消费商品时所感受到的满足程度 |
||
|
无差异曲线 |
两种商品或两组商品的不同数量组合对消费者所提供的效用是相同的。 |
||

资本资产定价模型
(1)资本资产定价模型的基本假设
资本资产定价模型建立在马科维茨模型基础上。
|
马科维茨模型的假定 |
①投资者希望财富越多越好 ②投资者能事先指导投资收益率的概率分布为正态分布 ③投资风险用投资收益率的方差或标准差表示 ④影响投资决策的主要因素为期望收益率和风险两项 ⑤投资者都遵守主宰原则(同一风险水平下选择收益高的,同一收益率水平下选择风险低的) |
①投资者是理性的 ②资本市场是完全有效的 |
|
资本资产定价模型的附加假设条件 |
⑥可以在无风险折现率R的水平下无限制地借入或贷出资金 ⑦所有投资者对证券收益率概率分布看法一致 ⑧所有投资者具有相同的投资期限 ⑨所有的证券投资可以无限细分 ⑩税收和交易费用可以忽略不计 ⑪所有投资者可以及时免费获得充分的市场信息 ⑫不存在通货膨胀,且折现率不变 ⑬投资者具有相同预期 |
(2)分离定理:投资者对风险的偏好状况与该投资者风险资产组合的最优构成是无关的。
(3)市场组合:在均衡状态下,每种证券在切点处投资组合都有一个非零的比例。

套利定价理论
套利定价理论假设:
①投资者有相同的理念;
②投资者是风险回避的,并且还要实现效用的最大化;
③市场是完全的,因此对交易成本等因素都不作考虑。

行为金融学
(1)投资者的非理性行为
|
行为 |
表现 |
|
过度自信 |
①投资者者过分依赖自己的信息忽视公司情况或其它投资者的信息 ②投资者审视信息时,注重能增强他们自信心的信息,忽视伤害其自信心的信息 |
|
反应过度和反应不足 |
反应过度:对一些消息过于重视造成行为过激 反应不足:也可称保守主义 |
|
损失厌恶 |
决策过程中更倾向于“避害”而非“趋利” |
|
处置效应 |
投资者长期持有亏损证券,迅速卖出盈利证券 |
|
神奇式思考 |
|
(2)羊群效应
金融市场中的“羊群行为”是指由于受其他投资者采取的某种投资策略的影响而采取相同的投资策略,即投资人的选择完全依赖于舆论(随大流),或者说投资人的选择是对大众行为的模仿,或者过度依赖于舆论,而不是基于自己所挖掘的信息。

资产配置
(1)资产配置的基本步骤

(2)资产配置的基本方法
历史数据法:假定未来与过去相似,以长期历史数据为基础,根据过去的经历推测未来的资产类别收益。
情景综合分析法:一般预测期间在3~5年。
(3)不同投资者其风险偏好和风险承受能力不同,投资者应根据自身情况配置构建不同类型和不同权重的资产组合。
(4)资产配置策略
①从范围上看,可分为全球资产配置,股票、债券资产配置和行业风格资产配置等。
②从时间跨度和风格类别上看,可分为战略性资产配置、战术性资产配置和资产混合配置等。
③从配置策略上可分为买入并持有策略、恒定混合策略、投资组合保险策略和动态资产配置策略等。

收益率
必要收益率=无风险收益率+风险收益率
名义收益率=(1+实际收益率)×(1+预期通货膨胀率)-1
实际收益率=(1+名义收益率)/(1+预期通货膨胀率)-1
预期收益率:
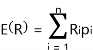
Ri为某一资产在第i种情形下的投资收益率;
pi为投资收益率可能发生的概率。

方差/标准差
方差/标准差:
投资组合实际收益率围绕预期收益率的波动。
预期收益率的标准差越大,预期收益率的分布越大,不确定性及风险越大。

协方差与相关系数
协方差与相关系数
|
协方差 |
①两个随机变量协同运动的程度和方向,取值(-∞,+∞) ②协方差>0,投资组合种的两种资产的收益同向变动 ③协方差<0,投资组合种的两种资产的收益反向变动 ④协方差=0,两种金融资产的收益没有相关关系 |
|
|
相关系数ρ |
①协方差的标准化,取值范围[-1,+1] ②相关系数为正,协方差为正;ρij=1,完全正相关 ③相关系数为负,协方差为负;ρij=-1,完全负相关 ④相关系数为0,协方差为0,表明两个随机变量不相关 |
|

贝塔系数
贝塔系数:
①度量特定资产(或资产组合)的系统性风险
②度量一种证券或投资组合相对总体市场的波动性
③β越大,投机性越强

无差异曲线
无差异曲线:两种商品或两组商品的不同数量组合对消费者所提供的效用是相同的。
