中级个人理财知识点：协方差与相关系数的概念是什么？

标准差一般是用来描述一维数据的，而实际生活中我们遇到的更多的是二维甚至是多维的数据，这里以二维数据为例介绍一下协方差和相关系数的概念。期望值分别为E[R₁]与E[R₂]的两个实数随机变量R₁与R₂之间的协方差定义为：

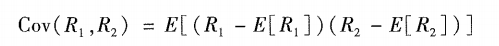
从上面的公式可以看出，方差是协方差的一种特殊情况，即当R₁与R₂两个变量相同的情况。

相关系数则定义为：

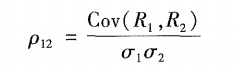
在金融领域，协方差的符号(正或负)可以反映出投资组合中两种资产之间的相互关系:如果协方差为正值，那就表明投资组合中的两种资产的收益呈同向变动趋势，即在任何一种经济情况下同时上升或同时下降；如果协方差为负值，则反映出投资组合中两种资产的收益具有反向变动的关系，即在任何一种经济情况下，一种资产的收益上升那么另一种资产的收益就会下降。如果协方差的值为零，就表明两种金融资产的收益没有相关关系。

相关系数等于两种金融资产的协方差除以两种金融资产的标准差的乘积。由于标准差总是正值，因此相关系数的符号取决于两个变量的协方差的符号。如果相关系数为正则表明两种资产的收益正相关；如果相关系数为负，说明两种资产的收益负相关;如果相关系数为零，说明两种资产的收益之间没有相关性。

更重要的是，可以证明相关系数总是介于-1和+1之间，这是由于协方差除以两个标准差乘积后使计算结果标准化。这有利于判断资产之间相关性的大小。