2014хЙДцфККщЋшщЋхцЌуцАхІчхЗЅчБЛуфИДшхЏцМшЏхЗ(2)
хЏМшЏЛяМ
шПх
Ѕх
ЈчцЈЁцшхКхЈчКПцЕшЏцЄхЅшЏхЗяМхЏцЅччцЁхшЇЃцхЙЖшЊхЈшЏх >> хЈчКПхщЂ
цЌцхЏМшЊ
фИушЇЃчщЂяМх
Б49хушЇЃчхКххКцЈчуцМчЎцЅщЊЄ
22у
(т )цБтГABCчхАшЇчхЄЇхАяМ
(т Ё)цБяМkABCчщЂчЇЏяМ
23у хЗВчЅхНцА?(x)=(x2+ax+2)ex(xяМaтR)яМ
(I)хНa=0цЖяМцБхНцА?(x)чхОшБЁхЈчЙA(1яМ?(1))хЄчхчКПцЙчЈяМ
(т Ё)хНa=-5/2цЖяМцБхНцА?(x)чцхАхМяМ
24ухЗВчЅцАх{an}чхnщЁЙхSn=nbnяМх ЖфИ{bn}цЏщІщЁЙфИК1яМх ЌхЗЎфИК2ччхЗЎцАхяМ
(I)цБцАх{an}чщщЁЙх ЌхМяМ
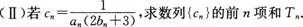
25у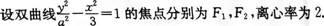
(I)цБцЄхцВчКПчцИшПчКПЮЙ1яМЮЙ2чцЙчЈяМ
(т Ё)шЎОAяМBххЋфИКЮЙ1яМЮЙ2фИчхЈчЙяМфИ2|AB|=5|F1F2|яМцБчКПцЎЕABфИчЙMчшНЈшПЙцЙчЈяМхЙЖшЏДццЏфЛфЙцВчКПяМ
22у

(т )цБтГABCчхАшЇчхЄЇхАяМ
(т Ё)цБяМkABCчщЂчЇЏяМ
23у хЗВчЅхНцА?(x)=(x2+ax+2)ex(xяМaтR)яМ
(I)хНa=0цЖяМцБхНцА?(x)чхОшБЁхЈчЙA(1яМ?(1))хЄчхчКПцЙчЈяМ
(т Ё)хНa=-5/2цЖяМцБхНцА?(x)чцхАхМяМ
24ухЗВчЅцАх{an}чхnщЁЙхSn=nbnяМх ЖфИ{bn}цЏщІщЁЙфИК1яМх ЌхЗЎфИК2ччхЗЎцАхяМ
(I)цБцАх{an}чщщЁЙх ЌхМяМ
25у
(I)цБцЄхцВчКПчцИшПчКПЮЙ1яМЮЙ2чцЙчЈяМ
(т Ё)шЎОAяМBххЋфИКЮЙ1яМЮЙ2фИчхЈчЙяМфИ2|AB|=5|F1F2|яМцБчКПцЎЕABфИчЙMчшНЈшПЙцЙчЈяМхЙЖшЏДццЏфЛфЙцВчКПяМ
уух ГцГЈччЙ:2014цшхПцПхЁЋцЅ/щЁЛчЅ цПч хшшЏцхА шхщЁЛчЅ чНцЅхЏч цЖцП
уухВхКшО хЏМ:щЋшЕЗчЙхВхКшЏщЂ фИхцЌхВхКшЏщЂ цшшЏщЂфИшНН ххЙДчщЂ шшЏхЄЇчКВ
чИх ГцЈш
- 2017хЙДцфККщЋшщЋшЕЗчЙцАхІ(ч)шшЏцЈЁцшЏщЂхчцЁцБцЛ04-07
- 2017хЙДцфККщЋшщЋшЕЗчЙцАхІ(ч)шшЏцЈЁцшЏщЂхчцЁфК04-06
- 2017хЙДцфККщЋшщЋшЕЗчЙцАхІ(ч)шшЏцЈЁцшЏщЂхчцЁх04-06
- 2017хЙДцфККщЋшщЋшЕЗчЙцАхІ(ч)шшЏцЈЁцшЏщЂхчцЁфИ04-05
- 2017хЙДцфККщЋшщЋшЕЗчЙцАхІ(ч)шшЏцЈЁцшЏщЂхчцЁфК04-05
| ПЮГЬзЈвЕУћГЦ | НВЪІ | дМл/гХЛнМл | УтЗбЬхбщ | БЈУћ |
|---|---|---|---|---|
| гяЮФ(ИпЦ№Еу)ОЋНВАр | ЕЫО§УФ | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
| гЂгя(ИпЦ№Еу)ОЋНВАр | Monica | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
| Ъ§бЇ(ЮФ)ОЋНВАр | ЭѕЗМ | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
| Ъ§бЇ(Рэ)ОЋНВАр | ТогзжЅ | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
| ДѓбЇгяЮФ(зЈЩ§БО)ОЋНВАр | ХЗбєАиСи | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
| гЂгя(зЈЩ§БО)ОЋНВАр | Monica | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
| ИпЕШЪ§бЇ(вЛ)(зЈЩ§БО)ОЋНВАр | ЭѕЬЮ | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
| ИпЕШЪ§бЇ(Жў)(зЈЩ§БО)ОЋНВАр | ТогзжЅ | ЃЄ150 / ЃЄ150 |  |
БЈУћ |
ИЈЕМПЮГЬ
- ИпЦ№Еу-Ъ§бЇ(ЮФЪЗВЦОРр)

- ЭѕЗМРЯЪІ
 УтЗбЪдЬ§
УтЗбЪдЬ§
- ИпЦ№Еу-гЂгя

- MonicaРЯЪІ
 УтЗбЪдЬ§
УтЗбЪдЬ§
- зЈЩ§БО-ДѓбЇгяЮФ

- ХЗбєАиСиРЯЪІ
 УтЗбЪдЬ§
УтЗбЪдЬ§
АрМЖНщЩм
ЬзВЭАќКЌЃКзЈЩ§БОVIPАр/ИпЦ№ЕуVIPАрЃЈКЌОЋНВ+ецЬтНтЮі+ФЃПМЕуЬт)
ЬзВЭгХЪЦЃК1ЁЂЫјЖЈКЫаФПМЕу
2ЁЂПМЧАЗЂЗХ2ЬзЪдЬт
3ЁЂУтЗбжибЇвЛДЮБЃеЯ
ХфЬзЗўЮёЃК1ЁЂУтЗбЬтПт
2ЁЂПЮГЬНВвх+ПЮМўЯТди+вЦЖЏПЮЬУ







 УтЗбЪдЬ§
УтЗбЪдЬ§ 




