重点、难点讲解及典型例题
一、债券的价值(★★★)
(一)债券价值(PV)的计算
通用的计算公式:PV=未来现金流出的现值
其中:未来的现金流出包括支付的利息和按债券面值偿还的本金,折现率为当时的市场利率或债券投资人要求的必要报酬率。
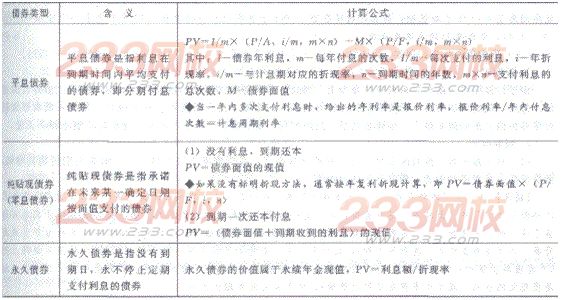
1.新发债券价值的计算
新发债券指的是在一级市场上新发行的债券,新发债券价值指的是发行时的债券价值。各种新发债券价值的计算方法如下:
【例题1·单选题】下列关于债券的说法中,不正确的是()。
A.债券的价值是发行者按照合同规定从现在至债券到期日所支付的款项的现值
B.平息债券的支付频率可能是一年一次、半年一次或每季度一次等
C.计算债券价值时使用的折现率,取决于未来的市场利率和现金流量的风险水平
D.纯贴现债券的购买人在到期日前不能得到任何现金支付,在到期日得到的现金支付等于面值
【答案】C
【解析】计算债券价值时使用的折现率,取决于当前的市场利率和现金流量的风险水平。
2.流通债券价值的计算
流通债券是指已经发行并在二级市场上流通的债券。相对于新发债券,流通债券的特点包括:(1)到期时间小于债券发行在外的时间;(2)估价的时点不在发行日,可以是任何时点,会产生“非整数计息期”问题。
【提示】这两个特点决定了流通债券价值的计算比较麻烦,教材中介绍了两种方法,第二种方法比较实用,所以只需要掌握第二种方法即可。在这种方法下,需要分两步:第一步是计算出流通债券在下一个付患日的价值(注意要考虑下一次支付的利息);第二步是把流通债券在下一个付息日的价值折现到估价时点的价值,这个时候涉及“非整数计息期”折现问题,需要注意,这个时候不能改变折现率,只能按照分数折现期折现。
【例题2·单选题】某债券的期限为5年,票面利率为8%,发行日为2010年4月1日,到期日为2015
年3月31日,债券面值为1000元,市场利率为10%,每半年支付一次利息(9月末和3月末支付),下列
关于该债券2011年6月末价值的表达式中正确的是()。
A.[40×(P/A,5%,8)+1000×(P/F,5%,8)]×(P/F,5%,1/2)
B.[40×(P/A,5%,7)+1000×(P/F,5%,7)]×(P/F,5%,1/2)
C.[40+40×(P/A,5%,7)+1000×(P/F,5%,7)]×(P/F,2.5%,1)
D.[40+40×(P/A,5%,7)+1000×(P/F,5%,7)]×(P/F,5%,1/2)
【答案JD
【解析】对于2011年6月末而言,未来还要支付8次利息,下一个付息日为2011年9月末。第一步:
计算该债券在2011年9月末的价值:未来要支付的8次利息在2011年9月末的现值=2011年9月末支付的利息+其他7次利息在2011年9月末的现值=40+40×(P/A,5%,7),到期时支付的本金l000在2011年9月末的现值=1000×(P/F,5%,7),所以,该债券在2011年9月末的价值=40+40×(P/A,5%,7)+1000×(P/F,5%,7);第二步:把该债券在2011年9月末的价值折现到2011年6月末,拆现期间为3个月,由于折现率5%是半年期的折现率,即一个折现期为半年(6个月),所以,3个月的折现期间为3/6=1/2个折现期,因此,该债券2011年6月末价值一该债券在2011年9月末的价值×(P/F,5%,1/2),即选项D的表达式正确。
(二)影响债券价值的因素
1.折现率
由于计算债券价值时,折现率在分母上,因此,在其他条件不变的情况下,折现率越高,债券价值越低。另外,随着到期时间(距离到期日的时间间隔)的缩短,由于折现期间越来越短,所以,折现率变动对债券价值的影响越来越小,即随着到期时间的缩短,债券价值对折现率特定变化的反应越来越不灵敏。
2.到期时间
(1)对于每间隔一段时间支付一次利息的债券而言,在折现率不变的情况下,随着到期时间的缩短,债券价值呈现周期性波动,最终等于债券面值。
【提示】溢价发行的债券在发行后价值逐渐升高,在付息日由于割息而价值下降,然后又逐渐上升,总的趋势是波动下降,最终等于债券面值;折价发行的债券在发行后价值逐渐升高,在付息日由于割息而价值下降,然后又逐渐上升,总的趋势是波动上升,最终等于债券面值;平价发行的债券在发行后价值逐渐升高(升至债券面值和一次利息之和),在付息日由于割息而价值下降(降为债券面值),然后又逐渐上升(升至债券面值和一次利息之和),总的趋势是波动式前进,最终等于债券面值。如果是连续支付利息(这是理想化的状态,现实中不存在这样的债券),则不会出现周期性波动。
(2)对于到期一次还本付息的债券而言,在折现率不变的情况下,随着到期时间的缩短,债券价值逐渐升高,最终等于债券的到期值。
(3)对于只需要到期按面值还本,不需要支付利息的债券而言,在折现率不变的情况下,随着到期时间的缩短,其价值逐渐接近面值。
3.利息支付频率
折价出售的债券,利息支付频率越快(即付息期越短),价值越低;溢价出售的债券,利息支付频率越快,价值越高;平价出售的债券,利息支付频率的变化不会对债券价值产生影响,债券价值一直等于债券面值。
【提示】对于分期付息的债券而言,有效年折现率=(1+报价折现率/m)m一1,有效年票面利率=(1+票面利率/m)m一1,其中,m是每年支付利息的次数。对于新发债券而言,如果有效年票面利率一有效年折现率,则债券价值一债券面值,平价出售;如果有效年票面利率高于有效年折现率,则债券价值高于债券面值,溢价出售;如果有效年票面利率低于有效年折现率,则债券价值低于债券面值,折价出售。对于某债券而言,决定债券价值与债券面值差额的是有效年票面利率与有效年折现率的差额,在有效年票面利率不等于有效年折现率的情况下,利息支付频率越快(即m的数值越大),有效年票面利率与有效年折现率的差额越大,从而导致债券价值与债券面值差额越大,所以,折价出售的债券,利息支付频率越快,债券价值越低于债券面值,即价值越低;溢价出售的债券,利息支付频率越快,债券价值越高于债券面值,即价值越高。对于平价出售的债券,有效年票面利率=有效年折现率,利息支付频率变化后,有效年票面利率仍然等于有效年折现率,因此,利息支付频率变化不会对债券价值产生影响,债券价值一直等于债券面值。


