第七章 期权价值评估
知识点：金融期权价值评估
（一）金融期权的价值因素
一个变量增加（其他变量不变）对期权价格的影响
|
变量 |
欧式看涨期权 |
欧式看跌期权 |
美式看涨期权 |
美式看跌期权 |
|
股票的市价 |
＋ |
－ |
＋ |
－ |
|
执行价格 |
－ |
＋ |
－ |
＋ |
|
到期期限 |
不一定 |
不一定 |
＋ |
＋ |
|
股价波动率 |
＋ |
＋ |
＋ |
＋ |
|
无风险利率 |
＋ |
－ |
＋ |
－ |
|
红利 |
－ |
＋ |
－ |
＋ |
（二）期权估值原理
1.复制原理
基本思想：构造一个股票和借款的适当组合，使得无论股价如何变动，投资组合的损益都与期权相同，则创建该投资组合的成本就是期权的价值。
2.套期保值原理（以购入股票、卖空看涨期权的情况为例）
（1）确定可能的到期日股票价格：
上行股价＝股票现价×上行乘数
下行股价＝股票现价×下行乘数
（2）根据执行价格计算确定到期日期权价值：
股价上行时期权到期日价值＝Max（上行股价－执行价格，0）
股价下行时期权到期日价值＝Max（下行股价－执行价格，0）
（3）计算套期保值比率：
套期保值比率＝（股价上行时期权到期日价值－股价下行时期权到期日价值）/（上行股价－下行股价）＝上、下行期权价值差异/上、下行股票价格差异
（4）计算投资组合的成本：
购买股票支出＝套期保值比率×股票现价
借款＝（到期日下行股价×套期保值比率－股价下行时看涨期权到期日价值）/（1＋无风险利率）
期权价值＝投资组合成本＝购买股票支出－借款
3.风险中性原理
风险中性原理：假设投资者对待风险的态度是中性的，所有证券的预期报酬率都应当是无风险利率。风险中性的投资者不需要额外的收益补偿其承担的风险。在风险中性的世界里，将期望值用无风险利率折现，可以获得现金流量的现值。
在这种情况下，期望报酬率符合下列公式：
期望报酬率＝（上行概率×上行时收益率）＋（下行概率×下行时收益率）
＝（上行概率×上行时收益率）＋（1－上行概率）×下行时收益率
假设股票不派发红利，股票价格的上升百分比就是股票投资的报酬率，因此：
期望报酬率＝（上行概率×股价上升百分比）＋下行概率×（－股价下降百分比）
根据这个原理，在期权定价时，只要先求出期权执行日的期望值，然后，使用无风险利率折现，就可以求出期权的现值。
（三）二叉树期权定价模型
1.单期二叉树模型。关于单期二叉树模型，其计算结果与前面介绍的复制组合原理和风险中性原理是一样的。
2.两期二叉树模型。如果把单期二叉树模型的到期时间分割成两部分，就形成了两期二叉树模型。由单期模型向两期模型的扩展，不过是单期模型的两次应用。
3.多期二叉树模型。
期数增加以后带来的主要问题是股价上升与下降的百分比如何确定问题。期数增加以后，要调整价格变化的升降幅度，以保证年报酬率的标准差不变。把年报酬率标准差和升降百分比联系起来的公式是：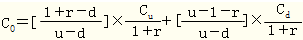
u＝1＋上升百分比＝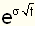
d＝1－下降百分比＝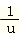
其中：e＝自然常数，约等于2.7183
σ＝标的资产连续复利报酬率的标准差
t＝以年表示的时间长度（每期时间长度用年表示）
（四）布莱克-斯科尔斯期权定价模型
1.计算公式
布莱克-斯科尔斯期权定价模型的公式如下：
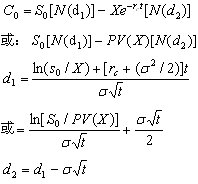
2.看跌期权估价
对于欧式期权，假定看涨期权和看跌期权有相同的执行价格和到期日，则下述等式成立：
看涨期权价格－看跌期权价格＝标的资产的价格－执行价格的现值
这种关系被称为看涨期权-看跌期权平价定理，利用该等式中的4个数据中的3个，就可以求出另外一个。
近期热点推荐：2015注会考后总结分析汇总 2016年注册会计师考试全面介绍
讲师辅导课程免费试听：233网校推出2016年注册会计师考试全程护航班！六门考试课程，四大辅导班型，5年无限制自由学习立即抢购>>。报名咨询热线：4000-800-233
交流区：一键加qq群信息跟网友一起来探讨考注会的心得：
（群：259245525）
