二、计算题
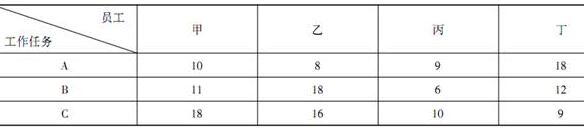
1. 某车间产品装配组有甲、乙、丙、丁四名员工,现有A、B、C三项任务需要完成。在现有生产技术组织条件下,每位员工完成每项工作所需要的工时如表1所示(单位:工时)。
请运用匈牙利法求出员工与任务的配置方法,以保证完成任务的总时间最短,并求出完成任务的最短时间。
表1 四名员工完成3项任务的工时统计表
【答案】
在应用匈牙利法解决员工任务合理指派问题时,应当具备以下两个约束条件:①员工数目与任务数目相等;②求解的是最小化问题,如工作时间最小化、费用最小化等。
本题中,员工数目大于任务数目,因此应虚拟一个任务D,并赋予各员工完成任务D的时间为0。此时,员工数目与任务数目相等。
具体计算过程如下:
(1)以各个员工完成各项工作的时间构造矩阵,得到矩阵一。
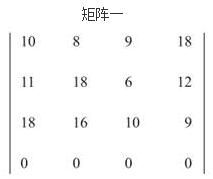
(2)对矩阵一进行行约减,即每一行数据减去本行数据中的最小数,得到矩阵二。

(3)画“盖0”线,即画最少的线,将矩阵二中的“0”全部盖住,得到矩阵三。

首先从含“0”最多的行或列开始画“盖0”线。
(注:“盖0”线的画法不唯一,如上述情况,可以画横线,也可以画竖线)
说明:进行约减时,可以进行行约减,也可以进行列约减,且“盖0”线的画法不唯一。因此,计算过程不唯一,最终矩阵的形式也不唯一。但是,最终的配置结果相同。
(4)求最优解。
①找只含一个“0”的行或列,将其打“√”。
②将其对应的行或列的其他“0”打“×”。
求解结果如矩阵四所示,即员工甲负责任务D,员工乙负责任务A,员工丙负责任务B,员工丁负责任务C,参照表1中员工完成任务时间汇总表,得出表2所示的员工配置最终结果。
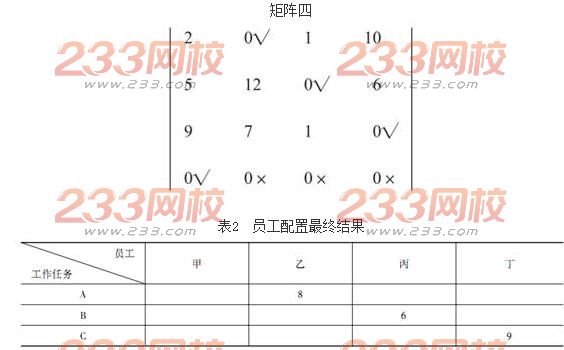
由以上分析可知,这三项任务分配给乙、丙、丁三位员工完成,其需要的总工时,即完成任务的最短时间为:8+6+9=23(工时)。


