2015年5月人力资源管理师三级专业技能真题及答案

　　二、计算题（18分）

　　某车间产品装配组有 成成、灰太狼、毛毛、三位员工，现有A、B、C、D四项任务，在现有生成技术组织条件下，每位员工完成每项工作所需要的工时如表1所示。由于现在有四项任务，而只有三个员工，可让一名效率较高的员工完成2项任务

　　请运用匈牙利法求出员工与任务的配置情况，以保证完成任务的总时间最短，并求出完成成任务的最短时间。

　　表1 每位员工完成四项工作任务的工时统计表 单位工时

　　解：

　　1)因为员工数小于任务数（四项任务，而只有三个员工），必有一名员工需要完成2项任务，故此将每个员工虚设为2人，即使虚拟的成成′,灰太狼′,毛毛′

　　2)现在为6名员工,4项任务,任务数小于员工数,故此需虚拟2项E和F任务，完成这两项任务的时间为0

　　3)现在为6名员工6个任务，可以使用匈牙利法求解，故此构成以下表格：

　　使用匈牙利法解：

　　1、构成矩阵

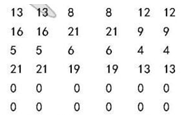
　　2、使每行每列至少包含一个零

　　用每行或每列的数分别减该行或该列的最小数即可，得以下矩阵

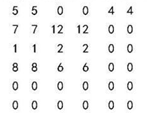
　　3、画盖零的直线数等于维数

　　a首先从零最多的行或列画盖零的直线

　　b直线数<维数，将进行数据转换

　　(找未被直线盖的最小数1；所有未被直线盖的数-1：两直线相交点+1)

　　构成以下矩阵

　　4求最优解

　　a找只有一个零的行或列(因为有3名员工虚拟的，故与员工本人数相同，即同一人的两个零可看成一个零)，将其打√

　　b将其对应的行或列的其它零打×

　　c将最后打√的零对应的敷(表格中)相加，即为最少工作时间

　　5　　　5　　　0√　　0 　　　5　　　5

　　6　　　6　　　11　　11　　　0×　　0√

　　0√　　0　　　1　　　1　　　0×　　0×

　　7　　　7　　　5　　　5　　　0√　　0

　　0×　　0×　　0×　　0×　　　1　　　1

　　0×　　0×　　0×　　0×　　　1　　　1

　　通过与表格数据对照，工作分配如下：

　　新航道负责c任务(5小时)，灰太狼负责A任务(8小时)，毛毛负责B任务(9小时)与D任务(13小时)，共完成所有任务最小时间为5+8+9+13=35小时

交流平台：人力资源考试qq群　233网校app下载

成绩查询：2015年5月人力资源管理师成绩查询时间

　快速通关：人力资源管理师如何通关？讲师解密新考点，锁定核心考点 精准押题提分