利率变化是影响债券价格的主要因素之一，久期和凸度是衡量债券价格随利率变化特性的两个重要指标。
经过长期研究，人们提出“久期”(Duration)的概念，把所有影响利率风险的因素全部考虑进去。这一概念最早是由经济学家麦考雷(F.R.Macaulay)于1938年提出的。
久期表示了债券或债券组合的平均还款期限，它是每次支付现金所用时间的加权平均值，权重为每次支付的现金流的现值占现金流现值总和的比率。久期用D表示。久期越短，债券对利率的敏感性越低，风险越低;反之，久期越长，债券对利率的敏感性越高，风险越高。
久期的计算有不同的方法。首先介绍最简单的一种，即平均期限(也称麦考利久期)。这种久期计算方法是将债券的偿还期进行加权平均，权数为相应偿还期的货币流量(利息支付)贴现后与市场价格的比值，即有：
D=1×w1+2×w2+…+n×wn
式中：
ci——第i年的现金流量(支付的利息或本金);
y——债券的到期收益率;
P——当前市场价格。
凸性( Convexity )是收益率变化 1
%所引起的久期的变化。用来衡量债券价格收益率曲线的曲度。。凸性越大，债券价格曲线弯曲程度越大，用修正久期度量的利率风险所产生的误差越大。
凸度的计算
①
P：债券价格
y：收益率或市场利率
t：债券期数
Ct：债券各期现金流
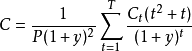
【例题】某债券的修正久期为3.5年，价格为98.50元，到期收益率为6%，则当利率下降 1%时，债券的价格将( )。
A.下降3.45元
B.上升3.45元
C.下降3.25元
D.上升3.25元
答案：B
