单代号网络计划图表示的方法和参数标注的形式和双代号网络计划图不一样,但是解网络图的计算方法和理解过程是一样的,所以,我们可以利用在“计算考点三:解双代号网络图”中学习过的解网络图思路来进行单代号网络计划图的学习和解题。
一、表示方法

单代号网络图时间参数的表示方法
二、解题思路
单代号网络图中每一个节点表示一项工作,把节点想象成车站,起点站只发车不进车,终点站只进车不发车,箭线为公交车行驶的线路,计算顺序按照节点编号从小到大。
三、解题方法
下面,就让我们通过这张单代号网络计划图来学习一下解单代号网络图的方法。
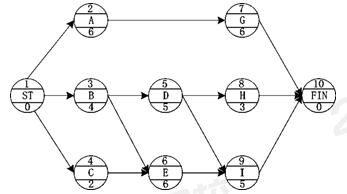
解题步骤:
【计算顺序按节点编号从“小 → 大”,算出最早开始时间、最早完成时间,并标在图上】
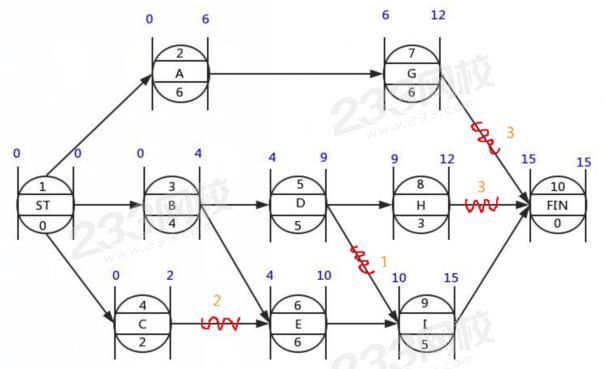
把节点想象成车站,该网络图一共10个车站,1号站为起点站,10号站为终点站。
(1)只有一趟车进了2号站,紧前工作最早完成时间是0,所以2号站最早开始时间为0,由于2号站持续时间为6天,所以2号站最早完成时间是第6天(0+6)。
(2)3号站和4号站只有一趟车进站,所以最早开始时间也是0,最早完成时间分别是第4天(0+4)和第2天(0+2)。
(3)5号站只有一趟车进站,所以最早开始时间是第4天,最早完成时间是第9天(4+5)。
(4)6号站有两趟车进站,B车第4天进站,C车第2天进站,要求两趟车都进站了6号站才能发车,所以6号站最早开始时间取大值,为第4天(即紧后工作的最早开始时间=各紧前工作的最早完成时间的最大值=Max【4,2】,唯一取大的情况)。 C工作和E工作之间等待了2天,在图中画上波形线,并写上“2“。
(5)同样方法算出其他站点的最早开始时间和最早完成时间,画在图上。工作之间有等待时间的,画上波形线,并写上等待时间(即为间隔时间LAG)。
(6)总工期:终点节点的最早完成时间为该网络计划图的总工期,为15天。
(7)关键线路:自始至终无波形线的线路为关键线路。所以这张单代号网络计划图的关键线路为1-3-6-9-10。
四、经典例题
【2017年真题】某单代号网络计划如下图,工作A、D之间的时间间隔是( )天。
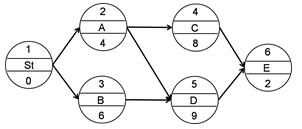
A. 0
B. 1
C. 2
D. 3
【233网校答案】C
【233网校解析】
按照以上的解题方法,可以解出下面这张单代号网络计划图:
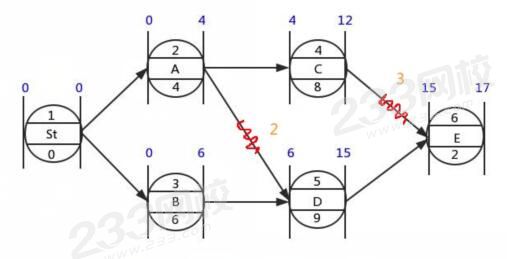
从图中可以看出,工作A、D之间的等待时间为2天,所以工作A、D之间的时间间隔即为2天,正确选项为 C。
(补充理解:时间间隔(LAG)=紧后工作的最早开始时间-本工作的最早完成时间)
【知识拓展】
(1)关键线路?
本图关键线路为:1-3-5-6(自始至终无波形线的线路)
(2)A工作的自由时差?
A工作有两个紧后工作(C和D),根据自由时差的公式可以算得:
A工作的自由时差=Min 【时间间隔LAG】= Min 【0,2】=0 (与紧后工作之间的时间间隔的最小值)
关宇老师对于这部分知识点的讲解十分生动且通俗易懂,不能很好理解的小伙伴可以多听几遍这部分的精讲课程,就能轻松掌握了。学好计算题的关键除开认真听老师讲解外,还得靠自己多练习,本篇中的题目要自己画一遍练一遍,才能记得更牢,学得更好!






























