万能解图神器，一网打尽所有网络图，考前必会！

2021版一建《项目管理》干货笔记-【点击】免费阅读

专题一：【时标网络计划图--万能解图法】

关键词：“找”、“看”“算”

【经典例题】下列双代号时标网络计划中，关键线路有（　　）条。

A．5      

B．4      

C．3      

D．2

解题思路：关键词是“找”，找那些自始至终没有波形线的线路。

第一条是：A→B→E→I→K。

第二条是：A→B→G→I→K。

第三条是：A→C→G→I→K。

【经典例题】某工程双代号时标网络计划如下图（单位：天） ，工作A总时差为（）天。

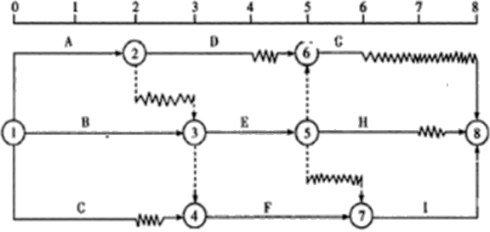
A．0　　 

B．2　　   

C．3　 　 

D．1

解题思路：本题考查的是总时差，关键词是“算”，就是该工作到终点的所有线路，波形线之和的最小值。

A工作的所有线路：共计5条，分别为：

（1）A-D-C  波型线之和为3

（2）A-E-C  波型线之和为3

（3）A-E-H  波型线之和为2

（4）A-E-I  波型线之和为2

（5）A-F-I  波型线之和为1

所以，波型线之和的最小值就是A工作的总时差。

专题二：【双代号网络计划图--万能解图法】

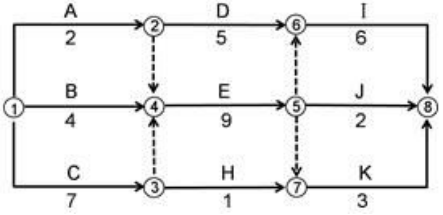
【经典例题】某工程双代号网络计划如下图，其计算工期是多少天？关键线路哪条？D工作自由时差和总时差？

【解题思路及步骤】

（1）把网络图想象成公交网络，一共有8个站，起点站为1号站，终点站为8号站。按编号从“小 → 大”依次解图。

（2）1号站，起点站，持续时间为0。

（3）2号站，只有A车进站，所以2号站发车时间为第2天（0+2）。

（4）3号站，只有C车进站，所以3号站发车时间为第7天（0+7）。

（5）4号站，有A、B、C三趟车进站，A车第2天进站、B车第4天进站、C车第7天进站，只有三趟车都到站，4号站才能发车，所以4号站发车时间为第7天。此时，A车要等待5天才能发车，B车要等待息3天才能发车，在图中画上波形线，并标记天数。

（6）5号站只有E车进，所以5号站发车时间为第16天（7+9）。

（7）同样方法，算出6号、7号站的发车时间及8号站的到站时间，并标注在图上；最终解完后的网络图如下：

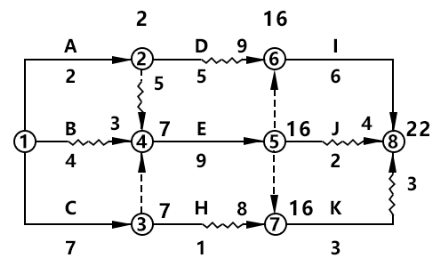
工期：8号站为终点站，终点站对应的时间即为网络图的总工期，总工期是22天。

关键线路：找自始至终无波形线的线路为关键线路：①-③-④-⑤-⑥-⑧。

D工作自由时差：看→ 本工作的波形线：为9天。

D工作总时差：算→ 该工作到终点的所有线路，波形线之和的最小值；只有1条，为D-I，波型线之和为9天。

专题三：【单代号网络计划图--万能解图法】

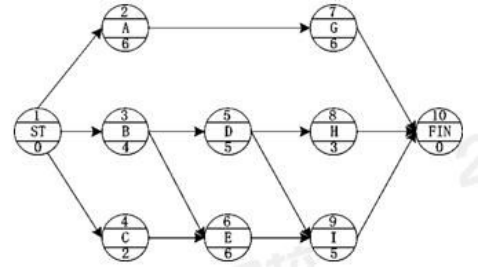
【经典例题】某工程单代号网络计划如下图，其计算工期是多少天？关键线路哪条？

【解题思路及步骤】

（1）把节点想象成车站，该网络图一共10个车站，1号站为起点站，10号站为终点站。

（2）1号车站，最早开始时间为0。

（3）2号车站，只有一趟车进站，紧前工作最早完成时间是0，所以2号车站的最早开始时间为0，由于2号站持续时间为6天，所以2号站最早完成时间是第6天（0+6）。

（4）3号站和4号站，均只有一趟车进站，所以最早开始时间也是0，最早完成时间分别是第4天（0+4）和第2天（0+2）。

（5）5号车站，只有一趟车进站，所以最早开始时间是第4天，最早完成时间是第9天（4+5）。

（6）6号车站，站有两趟车进站，B车第4天进站，C车第2天进站，要求两趟车都进站了6号站才能发车，所以6号车站最早开始时间为第4天，最早完成时间为第10天（4+6=10）。 C工作和E工作之间等待了2天，在图中画上波形线，并标上“2”。

（7）用同样方法算出其他站点的最早开始时间和最早完成时间，并标在图上。车站之间有等待的时间，标上波形线，并写上等待时间；解完的网络图如下：

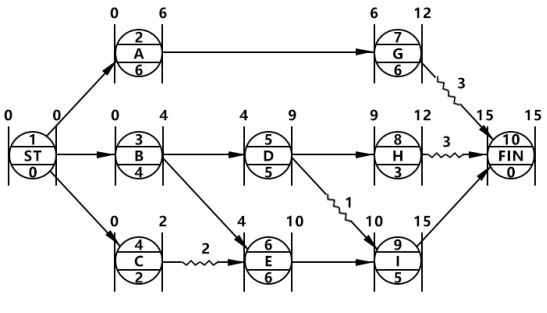
总工期：终点节点的最早完成时间为该网络计划图的总工期，为15天。

关键线路：自始至终无波形线的线路为关键线路。所以这张单代号网络计划图的关键线路为1-3-6-9-10。

该网络图的解图方法是【关宇老师】的杰作，点击马上试听＜＜＜

各位考友，对于这个知识点还有什么问题或疑问的，欢迎大家留言评论

零基础小白的钻石无忧班，学习无忧、考试无忧、保障无忧，放心点击加购﹥﹥﹥

温馨提示：文章由作者233网校-sunpeiyu独立创作完成，未经著作权人同意禁止转载。