（一）排列问题：从个元素中取个元素，需要考虑的顺序，用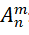表示。

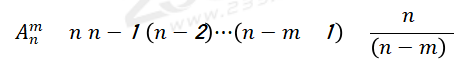
注意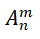：只表示排列数，而不表示具体的排列。

补充：规定0  1

基本排列问题例题

在某市物理竞赛中，一中、二中、三中三所学校分别有3名、2名、1名同学获得一等奖，将这6名同学排成一排合影，要求来自同一个学校的学生站在一起，则不同的排法共有（  ）种。

A. 12 B. 36 C. 72 D. 120 E. 720

【答案】C

（二）组合问题：从个元素中取个元素，无需考虑的顺序，用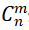表示。

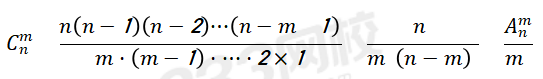
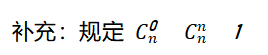
基本组合问题例题

飞腾公司近期组织员工出差培训，每回去两个人，从甲、乙、丙、丁、戊、己中任选两人出行，那么共有（  ）种不同的方案。

A. 5 B. 10 C. 15 D. 20 E. 25

【答案】C

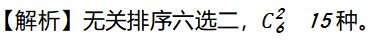
加法原理：完成一件事共有类办法；在第一类办法中有种不同的方法，在第二类办法中有种不同的方法，…在第类办法中有种不同的方法；那么完成这件事共有种不同方法。

乘法原理：完成一件事需要分成个步骤；完成第一步有种不同的方法，完成第二步有种不同的方法，…完成第步有种不同的方法；那么完成这件事共有种不同的方法。

解题关键：题干信息变化万千但不离其宗，我们需要从其中提取出关键的数学信息，用逻辑思维进行整合判断。将所有的题目拆解为“选取”和“排序”的过程，据此写对应表达式。

考向1 相邻问题——捆绑法：题目中规定某些元素必须相邻，解题时当作一个大元素来进行排列。

注意：较复杂题目有存在多个大元素的情况。

例题：第一中学甲班的6名学生一起去大剧院观看表演，安排有A、B两排座位，每排3个位置。其中小明和小红坐在一起的排法有（  ）种。

A. 48 B. 96 C. 120 D. 168 E. 192

【答案】E

【解析】A排：①②③  B排：④⑤⑥

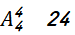小明和小红必须要坐在一起，他们只能坐①②、②③、④⑤、⑤⑥，共有种，其他四名同学在剩下四个位置排序种，故共有种。

考向2 相离问题——插空法：元素相离（即不相邻）问题，可先把无位置要求的几个元素全排列，再把规定的相离的几个元素插入上述几个元素的空位和两端。

例题：7人站成一排照相，若要求甲、乙、丙不相邻，则有（  ）种不同的排法。

A. 1020 B. 1040 C. 1140 D. 1220 E. 1440

【答案】E

【解析】除去甲、乙、丙三人余下四个人站位图：①A②B③C④D⑤，他们之间有①②③④⑤种空位可以分别插入甲、乙、丙三人，则有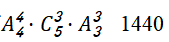种。

如果相邻与相离问题同时出现，则先考虑相邻元素，最后考虑相离元素。

考向3 隔板法：利用假定的隔板解决相同元素的分配问题。

题干标准形式一般表述为：将n个相同的元素分给个不同的对象，每个对象至少1个元素，求一共有多少种分法。

解题方法：将n个相同的元素排成一排，之间有n-1个空位，插入m-1块隔板就可以分成m份，最后共有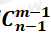种分法。

例题：赵一的妈妈来学校探望他，带了一篮香蕉让他和好朋友们共同分享。香蕉一共9支，分给寝室内包含赵一在内的四人，需保证每人至少有一支，那么总共有（  ）种不同的分法。

A. 40 B. 48 C. 56 D. 64 E. 72

【答案】C

【解析】利用隔板法，最后答案为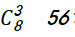种。

考向4 方幂法

审题重点：题干信息需要区分“可重复元素”和“不可重复元素”两类元素。

解题方法：一共有“可重复元素不可重复元素”种情况，即“可重复元素”为底数，“不可重复元素”为指数。

例题：从甲市到乙市的大巴上共有20人，沿途共7个停靠点（包括乙市在内），则不同的下车方法共有（  ）种。

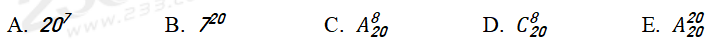
【答案】B

【解析】第1个人下车有7种方法，第2个人下车有7种方法……故总共有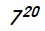种方法。