大题考察的内容大致可以分为9-11个类型，每年从中选出六个考察，有时候又会联合出题，例如定积分+微分方程，积分+极限等，综合性较强，除了最后一个题线性代数不变之外，其他的内容都是轮流考察的，这也是为什么老师讲课都是分模块，主要是各个击破，我们首先要基础打牢固，然后将所有的类型通过试题，多次训练，高分就会很稳定。
题型一：极限计算
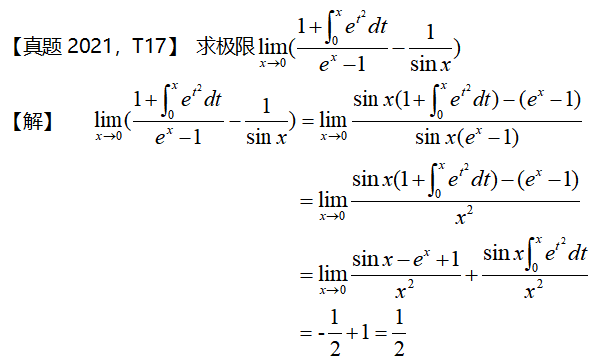
解题知识储备：
1.洛必达法则
2.带佩亚诺余项的泰勒公式如下：
题型二：多元函数极值（极值、求偏导数）
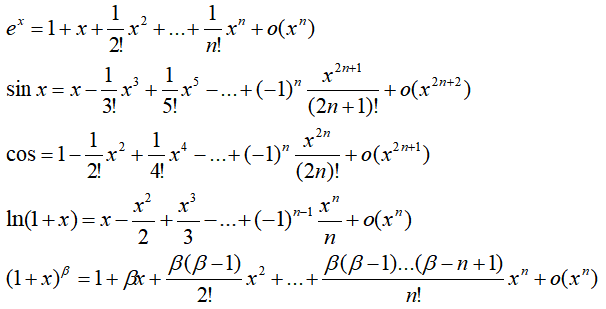
解题知识储备：
二元函数极值存在的充分条件
题型三：定积分计算（旋转体、表面积、弧长、应用题）
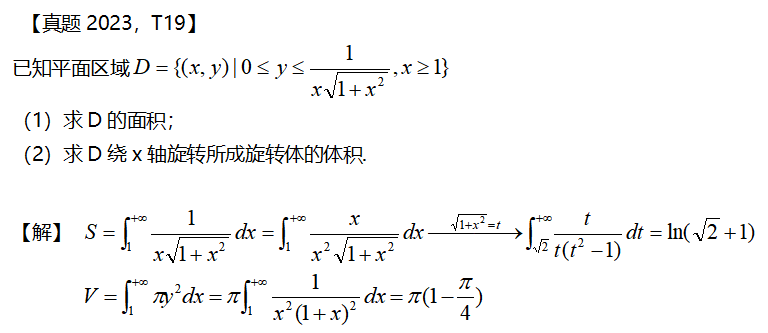
解题知识储备：
绕x轴旋转生成的旋转体的体积
题型四：二重积分
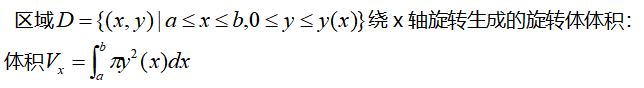
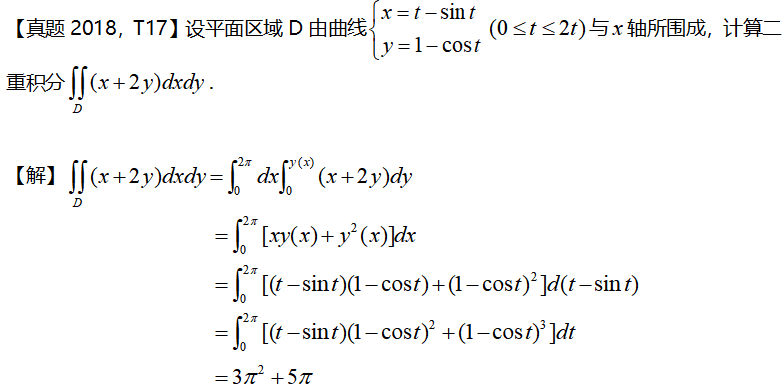
解题知识储备：
二重积分，一是理解定义，二呢学会画图，三善于利用性质，
本题算数学二，二重积分较难考题了，主要是写不出f(x)的函数表达式，掌握此题，二重积分没有难题。
题型五：中值定理
解题知识储备：
只含有一个ε，无其他字母的中值定理的解法，及辅助函数的构造方法。
题型六：线性代数（特征值、对角化、二次型、方程组的解、线性相关）
解题知识储备：
1.矩阵的等价
定义：设A与B均为m×n矩阵.如果矩阵A经过有限次初等变换可以化为矩阵B，则称矩阵A与B等价.
2. 非齐次线性方程组解集的结构
题型七：函数的特征（单调性、凹凸区间、渐近线、连续、恒成立证明）
解题知识储备：
极值的第一充分条件：
题型八：微分方程求解
解题知识储备：
二阶常系数线性微分方程求解：
题型九：极限存在性问题（数列、函数）
解题知识储备：
1.数学归纳法
2.由单调有界准则：单调递减有下界，数列收敛；
