一、大纲考点
1.平面图形
(1)三角形
(2)四边形(矩形、平行四边形、梯形)
(3)圆与扇形
二、大纲解读
根据历年的考试情况来看,本章所占的比重较大,难点主要在于图形的变换。由于本章与图形相关,所以解题时采用"*数形结合"来寻找捷径。另外,本章的公式比较多,知识点比较散,解题技巧性比较强,比如阴影面积的求解技巧等,所以在学习本章内容时,多归纳总结,寻求做题的突破。
【知识点】
一、平行线
一条直线和平行线的夹角
(1)同位角相等
(2)内错角相等
(3)同旁内角互补

2.直线被一组平行线截得的线段成比例

【重要考向】
1.求角度
【思路】注意平行线与其它特殊图形结合的所形成的角,不仅具有平行线角的关系,同时也要考虑到特殊图形角的关系.
2.求长度
【思路】根据平行直线的线段比例公式进行分析.
二、三角形
(一)角与边
【知识点】
1.三角形内角之和
1.三角形内角之和
∠1+∠2+∠3=π三角形外角等于不相邻的两个内角之和.
3.三角形三边关系
任意两边之和大于第三边,即a+b>c;
任意两边之差小于第三边,即a-b<c.
【重要考向】
1.求角度
【思路】注意平行线与其它特殊图形结合的所形成的角,不仅具有平行线角的关系,同时也要考虑到特殊图形角的关系
2.三边关系
【思路】根据三角形三边的关系来分析三角形的要求,任意两边之和大于第三边,两边之和小于第三边,只要满足其中一个就可以构成三角形.
(二)三角形面积
由思维导图+章节核心考点+历年真题汇总的干货笔记扫码即可免费试读>>>

(二)三角形面积
1.基本面积公式
(1)S=1/2ah,h是a边上的高,已知底和高,可以用此公式求面积.
(2)S=1/2absinC,C是边a和b的夹角.
【常见的sin值】
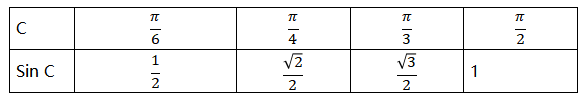
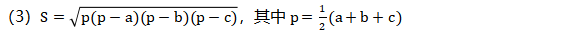
2.特殊三角形面积
(1)直角三角形

(2)等边三角形
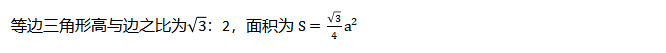
【重要考向】
1.利用底高关系计算面积
【思路】思路当两个三角形等高时,面积之比等于底之比;当两个三角形同底时,面积之比等于高之比;当两个三角形同底等高时,面积相等。
【2020.T10真题回顾】
1、如图,在∆ABC中,∠ABC=30°,将线段AB绕点B旋转至DB,使∠DBC=60°,则∆DBC与∆ABC的面积比值为( )。
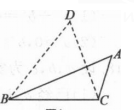
A.1
B.√2
C.2
D.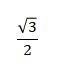
E.√3
2.利用夹角求面积
【思路】已知三角形两边及夹角,可以套公式求面积:S=1/2absinC.
【2017.T2真题回顾】
1、已知∆ABC和∆A'B'C'满足AB:A'B'=AC:A'C'=2:3,∠A+∠A'=π,则∆ABC和∆A'B'C'的面积之比为( )。
A.√2:√3
B.√3:√5
C.2:3
D.2:5
E.4:9
3.利用三边计算面积

【下载233网校题库APP,刷更多真题、模拟题及章节题>>】
考研复试>>【2022年考研国家线及34所自划线院校分数线汇总】【考研调剂系统】
考研初试>>【考研指南】 【考试信息查询系统】【报考条件查询系统】
资料领取>>【黄金备考资料免费领取】【0元领课】【干货笔记免费试读】
疯狂刷题>>【答题闯关赢奖品】【历年真题专题】【考试题库在线免费刷题】
在报考中遇到什么问题,欢迎进入“小编答疑版块”,在线向小编提问,我们将及时进行回复解答。
班主任督学+考前3个月密训+题库会员等!!
更多服务,你值得拥有!
阶段 | 主要内容 | 班级 |
规划阶段 | 定报考专业、院校,时间节点安排等,及各科考试内容综述与复习方法。 | |
基础阶段 | 课程+教辅+题库练习结合;知识点精讲精练,梳理各科考点;再配合学霸君《章节思维导图笔记》,及资深讲师带考经验,全方位带你高效熟记考点。 | |
强化阶段 | 课程+真题练习结合;资深讲师总结近10年真题中的高频考点及代表性真题深度剖析,再配合教辅,按章节带刷。 | |
冲刺阶段 | 课程+冲刺训练结合;全年热点时政、英语写作技巧与写作模板、政治主观题答题框架与答题技巧(结合冲刺8套卷+终极预测4套卷),层层带你锁分。 | |
临考阶段 | 考前2套内部试题;由资深带考老师命题及讲解,再结合模考大赛,来一次考前大比拼,知己知彼。 |
温馨提示:文章由作者233网校-liuyun独立创作完成,未经著作权人同意禁止转载。