多元函数的条件极值是考研数学的必拿分，因为题型变化不多，一是需要掌握好函数的条件，也就是φ(x,y)=0，齐次就是对于多元函数偏导的计算，其中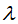
的求解是一个重点，可以利用克拉默法则，也可以用待定系数法，不过难度相对都不是很大。
二元函数z=f(x,y)在条件φ(x,y)=0下的极值：
方法一：拉格朗日法
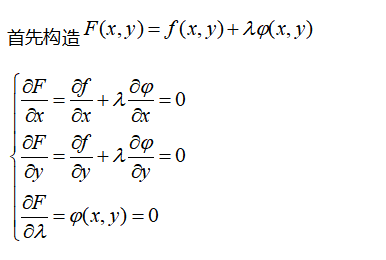
解得满足方程组所有点(x,y)，一一带入，取极值点即可。
【真题回顾，2018.T19】
将长为2 m的铁丝分成三段，依次围成圆、正方形和正三角形，三个图形的面积之和是否存在最小值?若存在，求出最小值
解：设分割后的三段铁丝的长分别为x，y，z，则x+y+z=2
方法二：参数方程法
2023考研如何上岸？资深讲师方浩、陈剑、赵鑫全为你护航，全套备考资料，复习有目标>>>
备考资料推荐
更多推荐
【证件照制作】
扫一扫二维码，加入考研上岸君微信
超多干货福利，就等你来领~ | 扫一扫二维码，关注233考研微信公众号
最新资讯第一时间知晓，备考经验技巧专栏传授 |
温馨提示：文章由作者233网校-chenyang独立创作完成，未经著作权人同意禁止转载。
