2021年硕士研究生招生考试试题
科目代码及名称: 618数学分析
适用专业(方向):070100 数学
请考生按规定用笔将所有试题的答案写在答题纸上,在此试题纸上答题无效
一、 计算题(每小题6分,共36分)
1. 求函数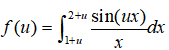 的导数
的导数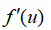
2. 求极限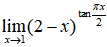
3. 求多元函数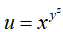 的全微分
的全微分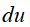
4. 求不定积分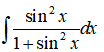
5. 求级数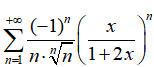 的收敛域
的收敛域
6. 求函数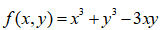 的极值
的极值
二、解答与证明题(每小题6分,共36分)
1. 设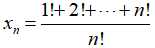 ,证明:
,证明: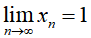
2. 证明: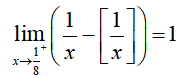
3. 设函数f(x)在闭区间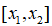 上可微,且
上可微,且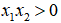 . 证明:
. 证明:
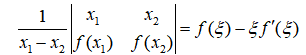 其中
其中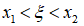
4. 若函数f(x)在无穷区间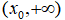 内可微,且
内可微,且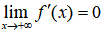 . 证明:
. 证明: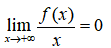
5. 讨论反常积分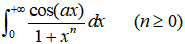 的敛散性
的敛散性
6. 证明:函数列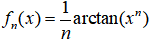 在区间
在区间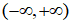 内一致收敛,但
内一致收敛,但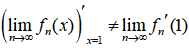
三、证明题(本题12分)
设函数f(x)在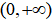 内连续,含参量反常积分
内连续,含参量反常积分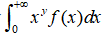 在y=a和y=b(a<b)时收敛. 证明:
在y=a和y=b(a<b)时收敛. 证明: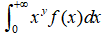 在[a,b]上一致收敛.
在[a,b]上一致收敛.
四、证明题(本题12分)
设f(x)在[a,b]上连续,对于区间[a,b]中的每一个点x,总存在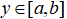 ,使得
,使得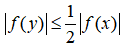 .
.
证明:至少存在一点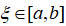 ,使得
,使得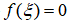 .
.
五、计算题(本题12分)
求三重积分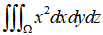 ,其中Ω是由抛物面
,其中Ω是由抛物面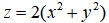 和
和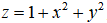 所围成的区域.
所围成的区域.
六、计算题(本题12分)
求积分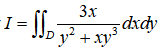 ,其中D为曲线
,其中D为曲线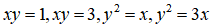 所围区域.
所围区域.
七、证明题(本题15分)
证明:级数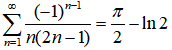
八、计算题(本题15分)
求第二型曲面积分
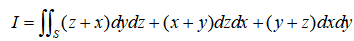
其中S是由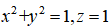 及三个坐标平面围成的立体在第一卦限的部分的表面,并取外侧。
及三个坐标平面围成的立体在第一卦限的部分的表面,并取外侧。
相关推荐:
扫一扫二维码,加入考研微信群
超多干货福利随机掉落,志同道合小伙伴随时交流~ | 扫一扫二维码,关注233考研微信公众号
最新资讯第一时间知晓,备考经验技巧专栏传授 |











