二、几何布朗运动
1.几何布朗运动的定义
几何布朗运动(GBM) (也叫做指数布朗运动) 是连续时间情况下的随机过程,其中随机变量的对数遵循布朗运动. 几何布朗运动在金融数学中有所应用,用来在布莱克-舒尔斯定价模型中模仿股票价格。法国数学家巴舍利耶在《投机交易理论》一文中提出股票价格遵循布朗运动。保罗·萨缪尔森1965年首次提出了股价S应遵循几何布朗运动。
2.相关方程式
1)股价S的随机微分方程形式为:
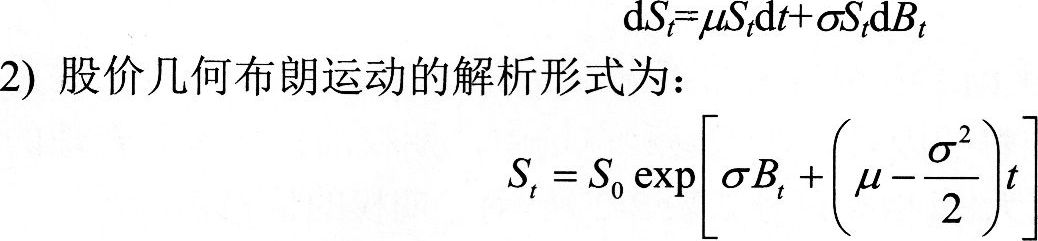
上式中,S表示t时刻的股价,μ、σ为常量,分别表示股票的期望收益率和波动率,Bt服从标准布朗运动。从公式可以看出,股票价格在短时期内的变动(即收益)来源于两个方面:①短时间内的预期收益率的变化;②随机正态波动项。
3、应用:
几何布朗运动在布莱克-舒尔斯定价模型被用来定性股票价格,因而也是最常用的描述股票价格的模型。使用几何布朗运动来描述股票价格的理由:
几何布朗运动的期望与随机过程的价格(股票价格)是独立的, 这与我们对现实市场的期望是相符的。
几何布朗运动过程只考虑为正值的价格, 就像真实的股票价格。
几何布朗运动过程与我们在股票市场观察到的价格轨迹呈现了同样的“roughness” 。
几何布朗运动过程计算相对简单。.
然而,几何布朗运动并不完全现实,尤其存在一下缺陷:
在真实股票价格中波动随时间变化 (possiblystochastically), 但是在几何布朗运动中, 波动是不随时间变化的。
在真实股票价格中, 收益通常不服从正态分布 (真实股票收益有更高的峰度('fatter tails'), 代表了有可能形成更大的价格波动).





























