三、B-S-M模型
1.布莱克一斯科尔斯一默顿(B-S-M)定价模型的主要思想
在无套利机会的条件下,构造一个由期权与股票所组成的无风险资产组合,这一组合的收益率必定为无风险利率r,由此得出期权价格满足的随机微分方程,进而求出期权价格。
2.B—S—M定价模型的基本假设
(1)标的资产价格服从几何布朗运动;
(2)标的资产可以被自由买卖,无交易成本,允许卖空;
(3)期权有效期内,无风险利率r和预期收益率μ是常数,投资者可以以无风险利率无限制借入或贷出资金;
(4)标的资产价格是连续变动的,即不存在价格的跳跃;
(5)标的资产的价格波动率为常数;
(6)无套利市场。
3.利用B—S—M模型定价
无红利标的资产欧式看涨期权C(看跌期权P)的定价公式为:
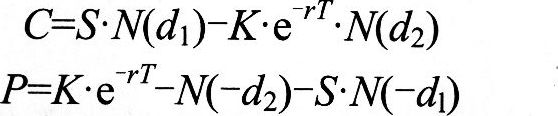

其他符号的含义如下:S为无收益标的资产的当前价格;σ无收益标的资产的价格波
动率;K为欧式看涨期权的执行价格;T为欧式看涨期权的到期时间;C为欧式看涨期权的价格;N(d)为标准正态概率值(具体值可以查正态概率值表),Ⅳ(-d)=1-N(d)。
4.对B-S-M定价模型的解释
(1)在风险中性的前提下,投资者的预期收益率μ用无风险利率r替代。
(2)N(d2)表示在风险中性市场中ST标的资产在T时刻的价格)大于K的概率,即欧式看涨期权被执行的概率。
(3)N(d1)是看涨期权价格对资产价格的导数,反映了很短时间内期权价格变动与其标的资产价格变动的比率。如果要抵消标的资产价格变化给期权价格带来的影响,一个单位的看涨期权多头就需要N(d1)单位的标的资产的空头加以对冲。
(4)资产的价格波动率拥于度量资产所提供收益的不确定性,经常采用历史数据和隐含波动率来估计。





























