线性回归模型
线性回归模型相关课程
线性回归模型考点解析
线性回归模型介绍
一元线性回归模型:yi=a+Bxi+μi(i=1,2,3,…,n) 其中，yi称为因变量或被解释变量；xi称为自变量或解释变量；μi是一个随机变量，称为随机(扰动)项；a和β是两个常数，称为回归参数。
多元线性回归主要用于分析影响因变量的因素，不仅涉及一个自变量，而且可能涉及多个自变量。例如，我们在分析一家公众公司的价值时，需要研究其多个财务指标，比如负债比例、资产回报率等指标序列（每个月指标）。这些指标构成公司价值（序列）的核心影响因素，我们定义公司价值（序列）为因变量时，这些财务指标（序列）就是自变量。
多元线性回归主要用于分析影响因变量的因素，不仅涉及一个自变量，而且可能涉及多个自变量。例如，我们在分析一家公众公司的价值时，需要研究其多个财务指标，比如负债比例、资产回报率等指标序列（每个月指标）。这些指标构成公司价值（序列）的核心影响因素，我们定义公司价值（序列）为因变量时，这些财务指标（序列）就是自变量。
多元线性回归分析模型【βk是参数，Xki的线性部分加上随机扰动项μi】
Yi=β0+β1β1i+β2β2i+…+βkXki+μi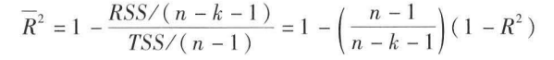
线性回归模型考点试题
的最小二乘回归结果显示，R2为0.92，总离差平方和为500，则残差平方和RSS为（）。
进行检验时，通常假定
服从（）。
大咖讲解：线性回归模型
相关性
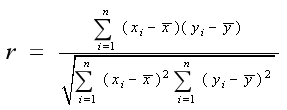
一元钱性回归分析
（一）一元线性回归模型的基本假定
设有如下一元线性回归模型：
yi：因变量或被解释变量；
χi：自变量或解释变量；
μi：一个随机变量，称为随机（扰动）项；
α，β：是两个常数，称为回归参数，
下标i：表示变量的第 i 个观察值或随机项
t检验
又称回归系数检验，步骤如下：
第一步：提出假设。设原假设 H0:β=0，备择假设H1:β≠0。
第二步：构造t统计量，即服从自由度为n-2的t分布：
一元线性回归分析的预测：点预测和区间预测
1.点预测。设回归模型为：
yi = α+β xi + μi (i=1, 2 ,3, ..., n)
假定在抽样期外的某预测期 f 中的自变量 xf 已知，上述模型适用于该预测期，这时因变量 yf =α+β xf + μf
其中，随机项满足基本假定。此时 yf 的预测值有两个，一个是期望值，一个是 yf 的点预测值。
多元钱性回归分析
多元线性回归模型分析一个因变量和几个自变量之间的关系。形式如下：
（二）多元线性回归模型的参数估计
同一元线性回归模型类似，可利用OLS估计多元线性回归模型的参数。此时有：
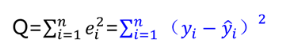
为使得残差平方和Q达到最小的必要条件为：
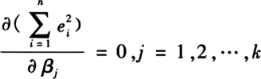
（三）多元线性回归模型的检验：
1.拟合优度检验
2.F检验（显著性检验）
3.t检验（回归系数检验）