教师资格综合素质每年考1道逻辑推理的选择题,难度不大,掌握以下4种题型即可!
一、包含关系(常考的两种)
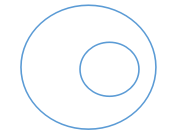
(1)真包含(于)关系
又称种属关系。a、b 两个概念,如果a概念的部分外延与b概念的全部外延相重合,那么a、b 两个概念具有真包含关系,读作a真包含b或b真包含于a。
(如:“学生”与“小学生”,“三角形”与“等边三角形”)
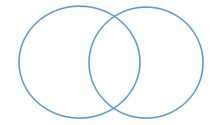
(2)交叉关系
a、b 两个概念,如果a概念只有部分外延与b概念的外延相重合,而b概念也只有一部分外延与a概念的外延相重合,那么a、b 两个概念间的关系就是交叉关系。
(如:“党员”与“教师”、“医生”与“博士”)
【真题再现】
下列选项中, 与"教师”和“戏剧爱好者”两概念的关系一致的是( )。
A.”军人”和”军医”
B.“杨树”和“柳树”
C.“蛋糕”和“面包”
D.“作家”和“画家”
二、命题推理
(1)假言命题
充分条件假言命题:“如果p,那么q”;(根据逆否命题,等价于“如果非q,那么非p”)
必要条件假言命题:“只有p,才q”。(根据逆否命题,等价于“只有非q,才非p”)
(2)负命题
一般形式:“并非p”,如“并非所有的人都是自私的”。原命题与负命题是矛盾关系。
以上命题的负命题形式:
① 并非“p且q”=非p或者非q
② 并非“p或q”=非p且非q
③ 并非“要么p,要么q”=“非p且非q”或者“p且q”
④ 并非“如果p,那么q”=p且非q
⑤ 并非“只有p,才q”=非p且q
⑥ 并非“并非p”=p
注意:原命题=逆否命题
如p→q =非 q→非p
【真题再现】
下列选项所表述的内容,包含在“只有经历过无数失败,才能懂得成功的艰辛”中的是( )。
A. 没有经历过无数失败,就无法懂得成功的艰辛
B. 如果经历了无数失败,就可以懂得成功的艰辛
C. 不懂得成功的艰辛,是因为没有经历过无数失败
D. 即使没经历过无数失败,也可以懂得成功的艰辛
已知题干“只有....才能”是必要条件假言判断,“懂得成功的艰辛”,推出“经历过无数失败”,根据逆否命题等价原命题的原理,可以从“没有经历过无数失败”推出“无法懂得成功的艰辛”,故选A。
BD项:选项是从“经历过无数失败”推出“懂得成功的艰辛”,不合题意,故不选。
C项:选项是从“无法懂得成功的艰辛”推出“没有经历过无数失败”,不合题意,故不选。
三、等差数列及变式(最常考,必须掌握)
形式 | 基本公式 | 举例 |
差数列基本形式 | 1.等差数列:一个数列从第二项起,每一项与前一项的差等于同一个常数。 第二项—第一项=第三项—第二项 2.二级等差数列:作差后得到的差数列是等差数列的称为二级等差数列。 (第二项—第一项)+常数(基本数列)=第三项—第二项 | 2,4,8,14,22 规律:c-b=b-a+2 |
差数列变式 | 作差得到其他基本数列或其变式,如等比数列、和数列。 第三项—第二项=2*(第二项—第一项)
| 2,4,8,16,32 规律:c-b=(b-a)*2 |
【真题再现】
找规律填数字是一项很有趣的游戏,特别锻炼观察和思考能力。下列各组数字,填入数列“1、3、7、13、23、( )、( )、107”空缺处,正确的是( )。
A. 28 57
B. 29 61
C. 37 59
D. 39 65
四、图形推理
1、位置类考点
(1)相对位置
考查相对位置时给出的图形一般含有多个构成部分,且构成部分之间具有一定的位置关系。
(2)移动、旋转、翻转
给出图形的显著特点是所有图形的构成元素完全相同,只是所处的位置不同。
2、结构类考点
(1)对称性
如果一个图形轴对称或者中心对称,我们就称这个图形对称。
(2)曲直性
曲直性描述的是一个图形的线条构成特点,如直线构成、曲线构成、直曲线混合构成等。
(3)封闭性
直观来说,封闭图形就是边缘由封闭线条围成的图形,否则,就是一个开放图形。
3、叠加类考点
此类图形推理题目的考查特点是其部分结构相同,但不完全相同,主要包括去同存异、去异存同等考点。
【真题再现】
将选项中的图形填到下面空格中,最符合格子中另外三个图形的一致性规律是( )
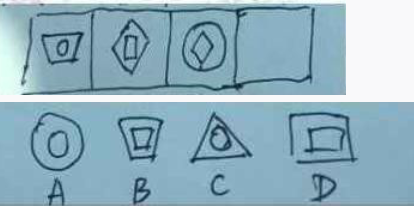
教师资格的任何备考疑问,欢迎留言交流~



