高中数学《奇函数的性质》
1、题目:奇函数的性质
2、内容:

3、基本要求
(1)让学生理解奇函数的含义,并能够利用奇函数的性质解决问题。
(2)教学中注意师生间的交流互动,有适当的提问环节,突出学生的学习主体地
(3)要求配合教学内容有适当的板书设计。
(4)请在10分钟内完成试讲内容。
答辩题目:
1定义在R上的奇函数,x=0处的函数值如何?为什么?
2本节课的教学目标是什么
二、考题解析
【教学过程】
(一)导入新课
回顾偶函数的定义及性质。
教师引导:偶函数是轴对称性质在函数图象中的一种特殊体现。除了轴对称,我们还学过什么样的对称性呢?
预设:还有中心对称。
引题:今天我们就来学习中心对称性质在函数图象中的一种特殊体现。
板书课题《奇函数的性质》。


【参考答案】
知识与技能:理解并掌握奇函数的定义及其性质,会灵活运用奇函数的性质解决问题。
过程与方法:经历奇函数概念的形成过程,体会从特殊到一般的数学思想方法,提高分析问题、解决问题的能力。
情感态度与价值观:积极参与学习过程,激发学习兴趣,提高学习信心,培养良好的数学学习习惯。
高中数学《平面与平面的位置关系》
1、题目:高中数学《平面与平面的位置关系》
2、内容:

3、基本要求:
(1)如果教学期间需要其他辅助教学工具,进行演示即可
(2)让学生结合生活实例理解平面与平面的位置关系
(3)教学中注意师生间的交流互动,有适当的提问环节,突出学生的学习主体地位
(4)要求配合教学内容有适当的板书设计。
(5)请在10分钟内完成试讲内容。
答辩题目:
1本节课在教材中有着什么样的地位和作用?
2在本节课的教学过程中,对于探究平面与平面的位置关系你是如何设计的?
二、考题解析
【教学过程】
(一)导入新知
回顾直线与直线、直线与平面的位置关系。提问:平面与平面的位置关系又是如何的呢?
引出课题——平面与平面的位置关系。

(三)课堂练习
如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论。
(四)小结作业
提问:今天有什么收获?引导学生回顾平面与平面的位置关系。
课后作业:练习题目。
【板书设计】

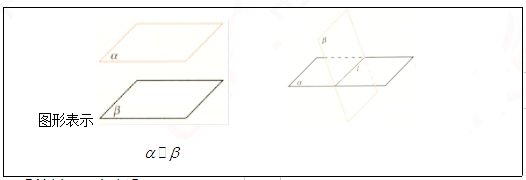
【答辩题目解析】
1.本节课在教材中有着什么样的地位和作用?
【参考答案】
《平面与平面的位置关系》选自人教版高中数学必修二第二章第一节,本节课主要讲解的是平面与平面的相交和平行,在此之前,学生已经学习了《平面》,认识了平面,了解了一些相关的公理,本节课是对学生原有的平面知识的拓展,也为今后学习空间立体几何打下基础,有着承上启下的作用。
2.在本节课的教学过程中,对于探究平面与平面的位置关系你是如何设计的?
【参考答案】
首先,设置了两个活动,一个是让学生将两本书看做两个平面,在移动和翻转的过程中观察它们的位置关系有几种,另一个是观察出示的长方体,思考围成长方体的六个面两两之间的位置关系有几种。通过这两个活动,让学生结合实例思考平面与平面的位置关系有几种,最后师生共同总结出平面与平面的位置关系,并说明如何用图形表示平面与平面的位置关系。接着,让学生自己尝试用图形表示。最后设置小组讨论,根据平面与平面的位置关系探究直线与直线的位置关系。整个教学过程,采用学生观察,师生总结,最后设置问题,将知识形成体系的方式来探究平面与平面的位置关系。
高中数学《余弦定理的证明》
1、题目:余弦定理的证明
2、内容:
基本要求
(1)让学生理解余弦定理的证明过程
(2)教学中注意师生间的交流互动,有适当的提问环节,突出学生的学习主体地位
(3)要求配合教学内容有适当的板书设计
(4)请在10分钟内完成试讲内容
1.利用余弦定理可以解决哪几类解三角形的问题?
2.如何备好一节课?
二、考题解析
【教学过程】
(一)导入新课
情景导入:多媒体展示修路工人开凿山地隧道的情境图。提问:“为了测量山地隧道的长度,工人先在山顶选一个位置A,量出A点到隧道两端的距离AB、AC及AB与AC的夹角,最后算出隧道长度。哪位同学能说说这是一个什么数学问题?”
预设:已知三角形两边及其夹角,去求另一边的数学问题。
提问:“那工人们是如何算出来的呢?”
引发认知冲入,从而引出课题。

(四)小结作业
小结:通过这节课的学习,你有什么收获?
作业:课后题。
【板书设计】

【答辩题目解析】
1.利用余弦定理可以解决哪几类解三角形的问题?
【参考答案】
(1)已知三边,求三个角。
(2)已知两边和夹角,求第三边和其他两个角。
2.如何备好一节课?
【参考答案】
一节好的数学课,要从以下几个方面准备:
首先,备教材,教材分析是教师备好课、上好课的基本保证,对教师顺利完成教学任务、提升教学质量有十分重要的意义。分析教材的过程既是教学科学把握教学内容、加深对教育理论的重要前提,更是教师进行教学研究的一种主要方法。
其次,备学生。教学的基本前提是为了学生而进行的教学,其根本目的在于促进学生的主动发展。因此在备课时要充分考虑所面对的学生特点。
最后,备教学方法。现代教学理论认为,在教学过程中,学生是学习的主体,教师是学习的组织者、引导者,教学的一切活动都必须以强调学生的主动性、积极性为出发点。
下载233网校APP,可获取教师资格证面试真题!
小编推荐:教师资格证面试考试流程 面试考生须知
真题推荐:历年教师资格证面试真题>>>
通关秘籍:教师资格证面试如何快速通关?233网校讲师将面试情景还原,助你一举攻下“结构化面试+试讲+答辩”三大内容,实战通关!免费体验>>


