二、简答题(本大题共5-13题,每题7分,共35分)
9.甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3道题,每人答对其中2道题就停止作答,即闯关成功,已知在6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是争。
(1)求甲、乙至少有一人闯关成功的概率;

12.《义务教育数学课程标准(2011年版)》,在各个学段中安排了4个部分的课程内容:“数与代数”“图形与几何”“统计与概率”“综合与实践”,其中“综合与实践”内容设置的目的在于什么?
13.简述初中数学新课程教学内容的特点。
三、解答题(本大题1小题,10分)
14.证明:连续的奇函数的一切原函数皆为偶函数:连续的偶函数的原函数中只有一个是奇函数。
四、论述题(本大题1小题,15分)
15.“数学学科内涵”是影响初中数学课程的主要因素之一。请以一元二次方程为例论述数学学科内涵的主要含义。
五、案例分析题(本大题1小题,20分)阅读案例,并回答问题。
16..案例:某同学在求反比例函数),=鱼,当x≤3时,求Y的取值范围时直接将x≤3代入y=2/3,得y≥2/3
问题:(1)该同学的解题过程哪步错了?分析原因:
(2)针对该生的情况,请你设计一个辅导教学片段,并说明设计意图:
(3)怎样防范这样的错误呢?
六、教学设计题(本大题1小题,30分)
17.在“一元二次方程根与系数的关系”一课上,某教师设计如下的教学过程:
一、探究规律
先填空,再找规律:
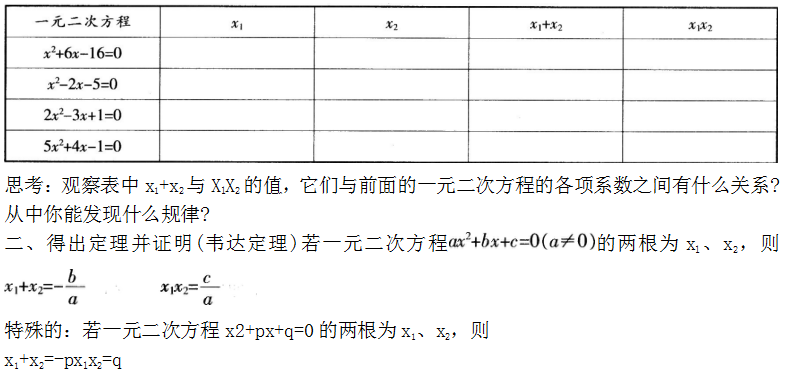
证明此处略(师生合作完成)
阅读上述教学设计片段,完成下列任务:
(1)请为此教学片段设计一个导入过程,并写出设计意图。(10分)
(2)分析该教师设计这两个环节的意图。(8分)
(3)请为此教学片段设计课堂练习并写出理由。(12分)

