一、单选题




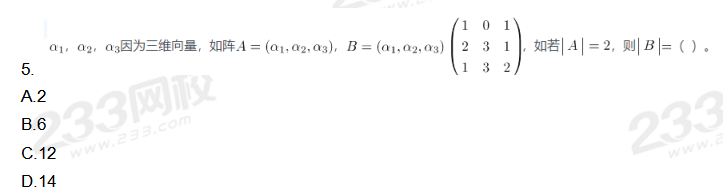
6.已知事件A发生的概率是1/3 , 事件B发生的概率是1/5 ,事件A和事件B同时发生的概率是1/15
则事件A和事件B同时都不发生的概率是( )
A.8/15
B.9/15
C.13/15
D.14/15
事件A不发生的概率为2/3,事件B不发生的概率为4/5,则事件A和事件B都不发生的概率为2/3*4/5=8/15。
7.南宋时期数学家秦九韶在数学上的主要成就是( )
A.二分法
B.辗转相除法
C.大衍求一术
D.割圆术
南宋数学家秦九韶著成『数书九章』十八卷,全书共81道题,分为九大类:大衍类、天时类、田域类、测望类、赋役类、钱谷类、营建类、军旅类、市易类。其中的"大衍求一术"在世界数学史上占有崇高的地位。秦九韶给出了理论上的证明,并将它定名为"大衍求一术"。
8.下列不能用尺规(无刻度的直尺和圆规)作图的是( ).
A.过一点作已知直线的垂线
B.已知底边和底边上的高作等腰三角形
C.已知斜边和直角边作直角三角形
D.作任意角的三等分线
尺规作图是指用无刻度的直尺和圆规作图。直尺的几何作用:作任意直线、连接任意两点、延长任意线段。圆规的几何作用:作任意圆(或弧)、截取任意长度。D项三等分线不符合。
二、简答题 (每题7分,共5题,共35分)

10.已知动点P与定点A (0,1,1) 的距离等于P到平面z=4距离的一半。
(1)求动点P的轨迹方程
(2)动点P的轨迹方程所表示的几何图形是什么?

11.不透明的袋子中有10个完全相同的乒兵球,分别标有数字1到10,从袋中随机摸出1个.球,记录标号后放回袋子.再随机摸出1个球,记录标号后也放回袋中。
(1)求两次摸球的标号之和是3的概率;
(2)求两次摸球的标号之和最大是7的概率
(1)P=2/100=1/50
(2)21/100
12.列举义务教育阶段一元二次方程的三种主要解法。

13.简述义务教育阶段统计内容中数据分析的主要过程,给出描述数据集中趋势和离散程度的统计量(各写出2个)。
数据分析的主要过程:收集、整理、描述、分析数据。
描述数据集中趋势的统计量:平均数,中位数、众数。
描述数据离散程度的统计量:极差、方差、标准差。
三、解答题 (每题10分,共1题,共10分)

四、论述题 (每题15分,共1题,共15分)
15.论述题
(1) 写出义务教务阶段涉及的不等式的性质(2条即可)
(2) 阐述不等式的性质与解一元一次不等式的关系,并举例说明
(1)不等式的性质
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变。如果a> b、那么a士c > b±c 。
性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变。如果a > b, c >0,那么ac > bc(或a/c>b/c)。
性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变。如果a>b,c<O,那么AC p c。< c<b
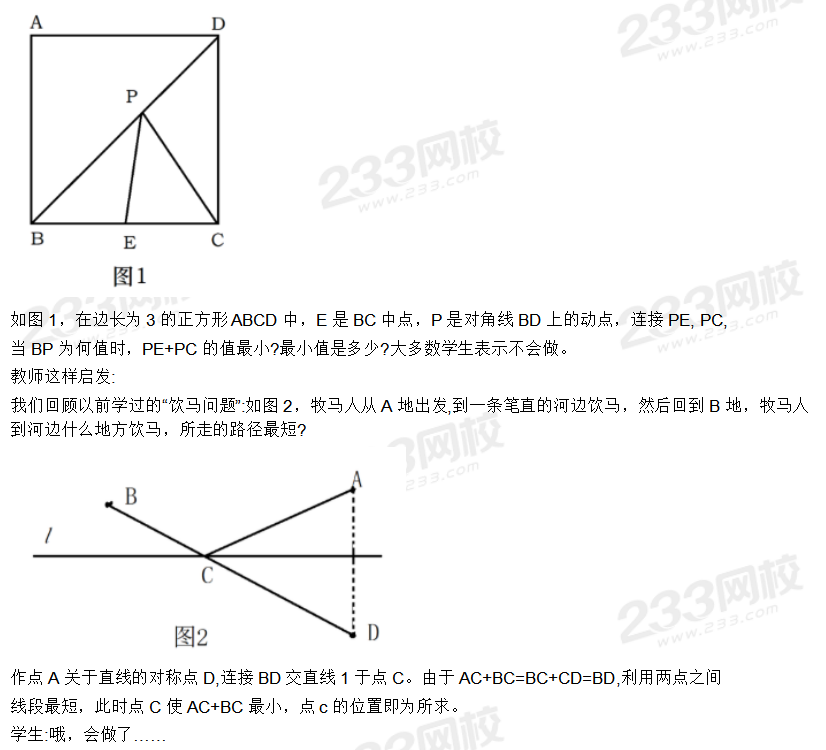
(1)给出该例题的求解过程 (10分)
(2)指出该教师对学生的启发有哪些合理和不足之处。(10分)
(1)在CD上找C关于AD为对称轴的点M连接EM交BD于P,即PE+PC值最小(8-10分)
(2) 合理之处:该教师注重启发式和因材施教,以学生已有经验为基础,面向全体学生,发挥了教师的主导作用。
不合理之处:该教师直接举例,对于学生的独立思考和主动探索方面的引导不够,不利于学生在合作交流中理解和掌握数学知识与技能。(8-10分)
六、 教学设计题 (每题30分,共1题,共30分)
17.下面是某教材有理数”一章中“绝对值”一节的内容片段:
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处 。它们的行驶路线相同吗?它们的行驶路程相等吗?

第一问
运用了分类与整合的数学思想方法:在解某些数学问题时,当被研究的问题包含了多种情况时,就必须抓住主导问题发展方向的主要因素,在其变化范围内,根据问题的不同发展方向,划分为若干部分分别研究.这里集中体现的是由大化小,由整体化为部分,由一般化为特殊的解决问题的方法,其研究的基本方向是“分”,但分类解决问题之后,还必须把它们整合在一起,这种“合—分—合”的解决问题的思想,就是分类与整合思想。
第二问
1.教学目标:
(1)知识与技能目标:借助数轴学生能够理解绝对值的概念;
(2)过程与方法目标:经历用数学符号表达绝对值的过程,发展学生抽象思维,提升解决问题的能力;
(3)情感,态度与价值观目标:体会数学与人类生活的密切联系,在学习过程中获得成就感。
2.教学重难点:
(1)教学重点:绝对值的概念。
(2)教学难点:从绝对值的几何定义中理解它的代数解释。
3.主要教学过程:
(1)情境导入
创设两辆汽车分别从同一处出发,分别向东,西方向行驶10千米的问题情境,提出问题:它们的行驶路程相等吗?
(2)新课教授
活动一:概念初步认识
结合数轴引出绝对值的概念。
活动二:概念加深理解
结合绝对值的定义,讨论a取正数,负数和0的不同情况。
(3)巩固练习
判断: 一个数的绝对值一定是正数。( )
一个数的绝对值不可能是负数。( )
(4)全课小结
师生共同总结绝对值的定义,渗透数形结合的思想。
(5)布置作业
在生活中观察发现只考虑绝对值的实例。
评分标准:
(1)字迹工整、美观;数学概念回答准确,相关知识点回答全面。(8-10分)
(2)字迹工整、美观;教学重难点突出;教学目标设定合理。(8-10分)
(3) 优秀:教学过程完整;教学内容设计合理、新颖;体现新课标理念;重点突出;实现教学目标(25-30分)
好:教学过程完整;教学内容设计基本合理;体现新课标理念;重点突出;实现教学目标(20-25分)
中等:教学过程完整;教学内容设计基本合理;基本体现新课标理念;重点不太突出;基本实现教学目标(15-20分)
较差:教学过程基本完整;教学内容设计不太合理;基本体现新课标理念;重点不突出;基本实现教学目标(10-20分)
差:教学过程不完整;教学内容设计不合理;没有体现新课标理念;重点不突出;没有实现教学目标(0-10分)
微信扫描免费领教资高频考点

考试题库>>2021年-2015年历年教师资格证真题在线模考
备考资料>>教资教学设计模板+思维导图下载
教资报考门槛将提升,珍惜报考机会,抓住新法改革前报考机会拿下证书。课程试听>>



