三、概念间关系
1.全同关系
全同关系又称同一关系,它是两个概念外延完全重合的关系。如“等边三角形”与“等角三角形”、“《呐喊》的作者”与“鲁迅”等。
2.真包含(于)关系
塞包含关系是指豫个概念外延部分重合的关系。a、b两个概念,如果a概念的部分外延与b概念的全部外延相重合,那么a、b两个概念具有真包含关系,也称种属关系,读作a真包含b或b真包含于a。如“学生,,与c。小学生”、“电影”与“数码电影”等。
3.交叉关系
交叉关系也是指两个概念的外延部分重合的关系。a,b两个概念,如果a概念只有部分外延与b概念的外延相重合,而b概念也只有一部分外延与a概念的外延相重合,那么a,b两个概念间的关系就是交叉关系。如“党员”与“教师”、“医生”与“博士”等。
4.全异关系
前面所讲的全同关系、真包含(于)关系和交叉关系都有一个共同点,那就是两个概念的外延至少有一部分相同。在逻辑中,通常将这些关系统称为相容关系。与相容关系相反的是不相容关系,也叫全异关系。
具有全异关系的两个概念的全部外延都不相同,完全没有重合的部分。全异关系又存在两种情况:矛盾关系和反对关系。
(1)矛盾关系
具有全异关系的两个概念a和b,同时包含于它们的属概念c当中,的全部外延。那么a与b具有矛盾关系,如“男人”与“女人”。
(2)反对关系
具有全异关系的两个概念a和b,同时包含于它们的属概念c当中,的全部外延.那么a与b具有反对关系。如“老人”与“小孩”。
如果a与b的外延之和等于c
如果a与b的外延之和小于c
四、概念间关系推理
前面我们已经介绍了几种概念间的关系类型,实际上对于一些简单的命题,我们都可以用概念间的关系表示,同时结合文氏图法进行推理。
下面对考试中常出现的命题所表示的概念间关系总结如下表:
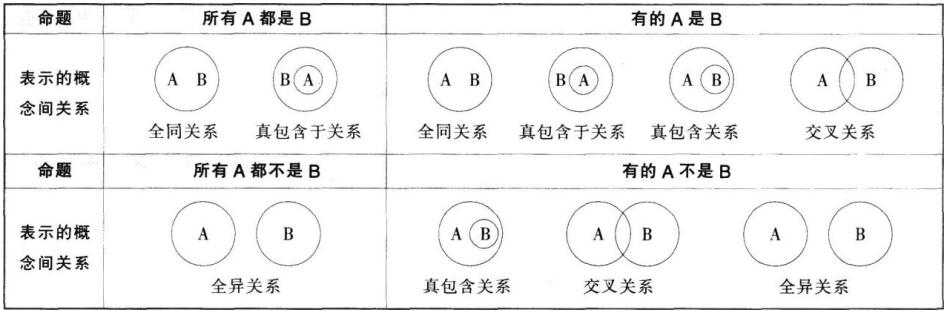
五、概括和限制
具有种属关系的概念的内涵与外延之间存在这样的关系:内涵较少的概念外延较大.内涵较多的概念外延较小。如“学生”和“中学生”相比,前者内涵比后者少,其外延比后者大。“学生”和“人”相比,前者内涵比后者多,其外延比后者小。
1.限制
限制是通过增加内涵.缩小外延.从属概念得到其种概念的逻辑方法,所以必须在有种属关系的概念之间进行。如“亚洲”不能限制为“东南亚”,因为两者不是种属关系。单独概念没有种概念,不能限制。如“螳螂”不能限制为“捕食的螳螂”。
2.概括
概括是通过减少内涵,扩大外延。从种概念得到其属概念的逻辑方法。概括也必须在具有种属关系的概念间进行。如“草”能概括为“植物”,不能概括为“草 原”。因为“草”和“植物”是种属关系。而“草”和“草原”是部分与整体的关系。最大类概念没有属概念,因而不能概括。如“事物”是最大类概念,不能概 括。
热点推荐:教师资格证考试中学综合素质考点归纳
通关必看:2017年教师资格证考试提前备考有妙招,233网校汇聚教师资格经验丰富讲师,为广大考生打造一次通关备考秘籍,点击查看>>

