一造《案例分析》决策树考点曾在2016年及2019年造价考试中出过题,而近几年来都没出现过,2023年出题的概率比较大,要求能够绘制决策树并计算与决策。
结合老师视频讲解,思路更清晰↓↓↓
决策树是以方框和圆圈为节点,并由直线连接而成的一种像树枝形状的结构,其中,方框表示决策点,圆圈表示机会点;从决策点画出的每条直线代表一个方案,叫作方案枝,从机会点画出的每条直线代表一种自然状态,叫作概率枝。(如下图所示)
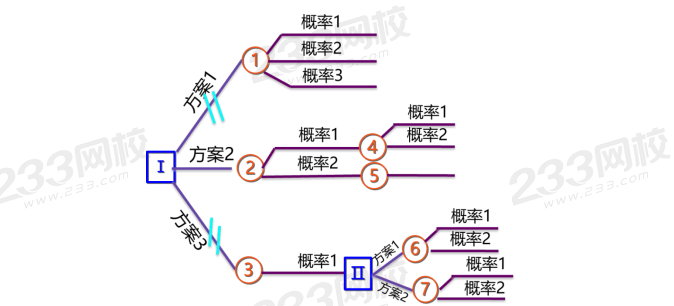
用决策点代表决策问题,方案枝代表可选方案,机会点(状态点)代表备选方案的经济效果,概率枝代表方案可能出现的各种概率,概率枝后面的数值代表不同方案在不同状态下可获得的损益值(又可包括机会点、决策点)。通过对各方案的期望值进行计算比较,为决策者提供决策依据。
绘图步骤及计算
1、决策树的绘制是自左向右(决策点和机会点的编号左小右大,上小下大),而计算则是自右向左。
2、各机会点的期望值计算结果应标在该机会点上方;
3、最后将决策方案以外的方案枝用两短线排除。
A企业结合自身情况和投标经验,认为该工程项目投高价标的中标概率为40%,投低价标的中标概率为60%。投高价标中标后,收益效果好、中、差三种可能性的概率分别为30%、60%、10%,计入投标费用后的净损益值分别为40万元、35万元、30万元;投低价标中标后,收益效果好、中、差三种可能性的概率分别为15%,60%,25%,计入投标费用后的净损益值分别为30万元、25万元、20万元;投标相关费用为5万元,A企业经测算、评估后,最终选择了投低价标,投标价为500万元。

机会点③期望值:0.3×40+0.6×35+0.1×30=36.00万
机会点④期望值:0.15×30+0.6×25+0.25×20=24.50万
机会点①期望值:36×0.4-0.6×5=11.40万
机会点②期望值:24.5×0.6-0.4×5=12.70万
机会点②的期望值大于①,故应选择投低标
如果你喜欢这篇文章,可以点击侧边【收藏★】下来哦~
温馨提示:文章由作者233网校-ljt独立创作完成,未经著作权人同意禁止转载。

