造价师工程造价管理基础理论与相关法规第3讲
3、等额支付系列情形
多次支付是指现金流量在多个时点发生，而不是集中在某一个时点上。用A t表示第t期末发生的现金流量大小，如果多次现金流量A t是连续序列流量，且数额相等，则具有这种特征系列的现金流量称为等额系列现金流量。
A——年金，发生在（或折算为）某一特定时间序列各计息期末（不包括零期）的等额资金序列的价值。对于等额系列现金流量，其复利计算方法如下：
（1）终值计算（即已知A求 F）。
F=A[(1+i) n -1]/i
式中[(1+i) n -1]/i 称为等额系列终值系数或年金终值系数，用符号（F／A，i，n）表示。于是上式又可写成：
F=A（F／A，i，n）
例：若在 10年内，每年末存入银行 1000万元，年利率为 8％，问 10年后本利和为多少？
解：由F＝A（F／A，i，n）＝1000（F／A，8％，10）
从附录中查出（F／A，8％，10）为14.487，代入式中得：F＝1000 × 14.487＝14487（万元）
(2)现值计算（即已知A求P）。
P=A[(1+i) n -1]/[i(1+i) n]
式中：[(1+i) n -1]/[i(1+i) n]称为等额系列现值系数或年金现值系数，用符号（P／A，i，n）表示。于是上式又可写成：
P＝A（P／A，i，n）
例：若希望在5年内每年收回1000万元，当利率为10％时，则开始需一次投资多少万元？
解：由P＝A（P／A，i，n）＝1000（P／A，10％，5）
从附录中查出系数（P／A，10％，5）为3．7908，代入上式得：P＝1000×3．7908＝3790．8（万元）
(3)资金回收计算（已知P求A）。
等额系列资金回收计算是等额系列现值计算的逆运算。
A=Pi(1+i) n /[(1+i) n -1]
式中：i(1+i) n /[(1+i) n -1]称为等额系列资金回收系数，用符号（A／P，i，n）表示。于是，上式又可写成：
A＝P（A／P，i，n）
例：若投资1000万元，每年收回率为8％，在10年内收回全部本利，则每年应收回多少？
解：由A＝P（A／P，i，n）＝1000（A／P，8％，10）
从附录中查出系数（A／P，8％，10）为0．14903，代入上式得：
P＝1000 × 0．14903＝149．03（万元）
(4)偿债基金计算（已知F求A）。同样，偿债基金计算是等额系列终值计算的逆运算，故可得：
(4)偿债基金计算（已知F求A）。同样，偿债基金计算是等额系列终值计算的逆运算，故可得：
A=Fi/[(1+i) n -1]
式中：i/[(1+i) n -1]称为等额系列偿债基金系数，用符号（A／F，i，n ）表示。则上式又可写成：
A＝F（A／F，i，n）
例：若想在第5年年底获得1000万元，每年存款金额相等，年利率为 10％，则每年需存款多少？
解：由A＝F（A／F，i，n）＝1000（A／F，10％，5）
从附录中查出系数（A／F，10％，5）为0．1638，代入上式得：P＝1000×0．1638＝163．8（万元）
现将以上计算公式总结如下表：中国注册造价工程师考试网(www.zaojiashi.com)提供.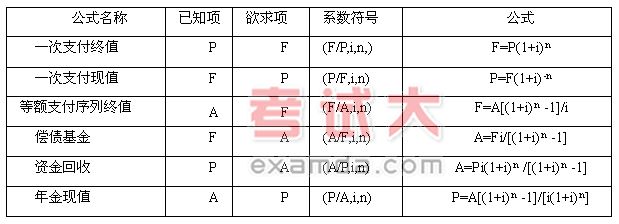
责编：虫
相关阅读
-
造价师管理基础理论与相关法规第1讲
-
造价师管理基础理论与相关法规第2讲
-
造价师管理基础理论与相关法规第4讲
-
造价师管理基础理论与相关法规第5讲
-
造价师管理基础理论与相关法规第6讲
-
造价师管理基础理论与相关法规第7讲
-
造价师管理基础理论与相关法规第8讲
-
造价师管理基础理论与相关法规第9讲
-
造价师管理基础理论与相关法规第10讲
-
造价师管理基础理论与相关法规第11讲
-
造价师管理基础理论与相关法规第12讲
-
造价师管理基础理论与相关法规第13讲
下载233网校APP
- 报考咨询 专业师资
- 课程学习 资料下载
- 免费题库 考前点题