【考点一】货币时间价值
今天的一块钱为什么比明天的一块钱更值钱?因为今天的一块钱可以拿去投资和再投资。
在日常生活中,即是【下图来自葛广宇老师精讲班】

上述图示就是货币时间价值的含义。
货币时间价值,是指在①没有风险和②没有通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值。
(一)衡量指标
通常使用相对数表示货币的时间价值,即用增加的价值占投入货币的百分数来表示,用相对数表示的货币时间价值也称为纯粹利率(简称纯利率)。
【注意】通过货币时间价值的含义,我们可以知道:
(1)纯利率是在没有通货膨胀、无风险情况下资金市场的平均利率。
(2)没有通货膨胀时,短期国库券的利率可以视为纯利率(以国家信誉作保障,基本上视为无风险利率)。
(二)作用:将某一时点的货币价值金额折算为其他时点的价值金额。
基于此,不同时点的货币不再具有可比性,要进行比较,必须转化到同一时点。
也就是说,如果要将今天的一块钱和明天的一块钱作比较,就必须把明天的一块钱折现到今天。
既然今天的一块钱>明天的一块钱,我们就可以知道,折现的过程是一个“缩水”的过程。
那么如何将货币转化到同一时点进行比较呢?要么把货币都放到“现在”这个时间进行比较——求现值;要么都放到未来进行比较——求终值。
【考点二】计息方式
单利 | ①按固定的本金计算利息 ②持有期间本金不变,各期利息不变(不对产生的利息计息) |
复利(俗称“利滚利”) | ①不仅对本金计算利息,还对利息计算利息 ②持有期间本金是变化的,各期利息也是变化的 |
【考点三】复利终值和现值(财管该科几乎不会用到单利)

【注意】
①复利是一个算次方的问题,而单利是一个乘法问题。即:
现存入本金100元,银行存款利率是8%,问三年后连本带利能从银行取出多少钱?
单利计息:能取出的金额=本金×(1+利率×期数)=100×(1+8%×3)=124(该思路在后续的学习中能用到,比如到期一次还本付息的债权)。
复利计息=100×(1+8%)3=125.97
②折现只能用复利折现。
③若每年计息不止一次时(即计息期短于一年),只要将年利率调整为计息期利率(名义利率/每年复利计息次数),将年数调整为期数即可,以后的系数处理方法相同。
【考点四】年金终值和现值
(一)年金的含义
①间隔期相等的系列等额收付款项。
②三个要点:定期(间隔期相等,可以不是一年,例如季度、半年度等)、等额、系列款项。
(二)年金的形式
①普通年金
②预付年金
③递延年金
④永续年金
(三)四种年金形式的计算公式
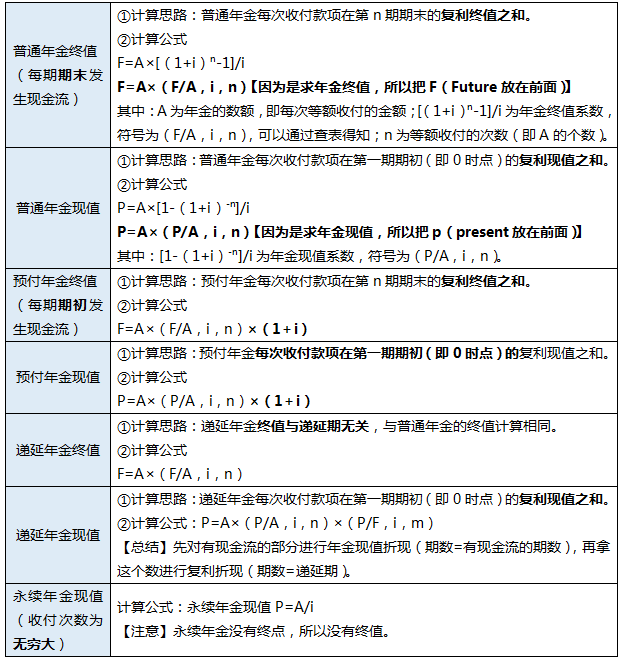
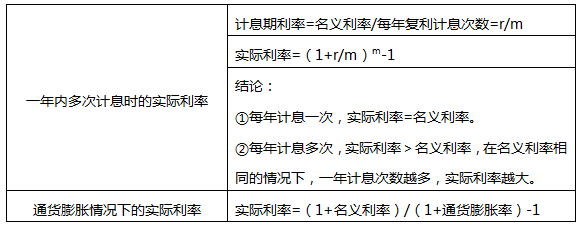
【考点五】实际利率的计算
温馨提示:文章由作者233网校-chenyayu独立创作完成,未经著作权人同意禁止转载。

