(一)均值:设一组数据为X1,X2,...,Xn,平均数的计算
(二)中位数——先排序再找中间位置
设一组数据为X1,X2,…,Xn,按从小到大顺序为X(1),X(2),…,X(n),则中位数为:
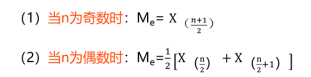
(三)众数
众数是指一组数据中出现次数(频数)最多的变量值。
(一)方差
1.对于总体数据(N为总体规模)


3.结论
(1)标准差的大小不仅与数据的测度单位有关,也与观测值的均值大小有关,不能直接用标准差比较不同变量的离散程度。
(2)离散系数消除了测度单位和观测值水平不同的影响,可以直接用来比较变量的离散程度。
(一)偏态系数
1.如果偏态系数等于0,说明数据的分布是对称的;
2.如果偏态系数为正值,说明分布为右偏的。
(1)取值在0和0.5之间说明轻度右偏;
(2)取值在0.5和1之间说明中度右偏;
(3)取值大于1说明严重右偏。
3.如果偏态系数为负值,说明分布为左偏。
(1)取值在0和-0.5之间说明轻度左偏;
(2)取值在-0.5和-1之间说明中度左偏;
(3)取值小于-1说明严重左偏。
4.偏态系数的绝对值越大,说明数据分布的偏斜程度越大。
(二)标准分数
1.标准分数可以给出数值距离均值的相对位置,计算方法是用数值减去均值所得的差除以标准差。
2.数据服从对称的钟形分布时,经验法则表明:
(1)约有68%的数据与平均数的距离在1个标准差之内;
(2)约有95%的数据与平均数的距离在2个标准差之内;
(3)约有99%的数据与平均数的距离在3个标准差之内。
3.对于服从对称的钟形分布的标准分数:
(1)约有68%的标准分数在[-1,+1]范围内;
(2)约有95%的标准分数在[-2,+2]范围之内;
(3)约有99%的标准分数在[-3,+3]范围之内。
1、Pearson相关系数的取值范围在+1和-1之间,即-1≤r≤1。
(1)若0<r≤1,表明变量X和Y之间存在正线性相关关系;
(2)若-1≤r<0,表明变量X和Y之间存在负线性相关关系;
(3)若r=1,表明变量X和Y之间为完全正线性相关;
(4)若r=-1,表明变量X和Y之间为完全负线性相关;
(5)当|r|=1时,变量Y的取值完全依赖于X;
(6)当r=0时,说明Y和X之间不存在线性相关关系。
2、根据实际数据计算出的r,其取值范围一般为-1<r<1。
在说明两个变量之间的线性关系的强弱时,根据经验可相关程度分为以下几种情况:
(1)当|r[≥0.8时,可视为高度相关;
(2)当0.5≤|r|<0.8时,可视为中度相关;
(3)当0.3≤|r|<0.5时,可视为低度相关;
(4)当|r|<0.3时,说明两个变量之间的相关程度极弱可视为无线性相关关系。
基本方法 | 适用条件 |
简单随机抽样 | 这种抽样方法的适用条件是:①抽样框中没有更多可以利用的辅助信息;②调查对象分布的范围不广阔;③个体之间的差异不是很大。 |
分层抽样 | 分层抽样的应用条件是:抽样框中有足够的辅助信息,能够将总体单位按某种标准划分到各层之中,实现在同一层内各单位之间的差异尽可能地小,不同层之间各单位的差异尽可能地大。 |
系统抽样 | - |
分阶段抽样 | 在大范围的抽样调查中,采用多阶段抽样是必要的。 |
整群抽样 | 应用整群抽样时,要求各群有较好的代表性,即群内各单位的差异要大,群间差异要小;整群抽样特别适合于对某些特殊群结构进行调查。 |
1.只涉及一个自变量的一元线性回归模型可以表示为:
Y=β0+β1X+ε
式中:β0和β1为模型的参数。
(1)Y是X的线性函数(β0+β1X)加上误差项ε。
(2)β0+β1X反映了由于X的变化而引起的Y的线性变化。
(3)误差项ε是个随机变量,反映了除X和Y之间的线性关系之外的随机因素对Y的影响,是不能由X和Y之间的线性关系所解释的Y的变异性。
2.描述因变量Y的期望E(Y)如何依赖自变量X的方程称为回归方程。
(1)一元线性回归方程的形式为:
E(Y)=β0+β1X
(2)一元线性回归方程的图示是一条直线,β0是回归直线的截距,β1是回归直线的斜率,表示X每变动一个单位时,E(Y)的变动量。
1.决定系数R2,也称为拟合优度或判定系数,可以测度回归模型对样本数据的拟合程度。
2.决定系数是回归模型所能解释的因变量变化占因变量总变化的比例,取值范围在0到1之间。
(1)决定系数越高,模型的拟合效果就越好,即模型解释因变量的能力越强。
(2)如果所有观测点都落在回归直线上,R2=1,说明回归直线可以解释因变量的所有变化。
(3)R2=0,说明回归直线无法解释因变量的变化,因变量的变化与自变量无关。
(4)现实应用中R2大多落在0和1之间,R2越接近于1,回归模型的拟合效果越好;R2越接近于0,回归模型的拟合效果越差。
(一)绝对数时间序列序时平均数的计算
时期序列 | 简单算术平均 | ||
时点 序列 | 连续时点 (以天为时间单位) | 逐日登记逐日排列 | 简单算术平均 |
指标值变动时才登记 | 加权算术平均 | ||
间断时点 | 间隔时间相等 | 两次平均:均为简单算术平均 | |
间隔时间不相等 | 两次平均: 第一次简单算术平均 第二次加权算术平均 | ||
(二)相对数或平均数时间序列序时平均数
计算思路:
(1)分别求出分子指标和分母指标时间序列的序时平均数,然后再进行对比。
(2)分子指标和分母指标时间序列的序时平均数,参照绝对数时间序列序时平均数的计算。
(一)增长量=报告期水平-基期水平
1.逐期增长量:报告期水平与前一期水平之差。计算公式为:∆i=yi-yi-1
2.累计增长量:报告期水平与某一固定时期水平(通常是时间序列最初水平)之差。
(二)平均增长量

(一)发展速度
1、发展速度=报告期水平/基期水平
定基发展速度=报告期水平/某一固定时期水平
环比发展速度=报告期水平/前一时期水平
2.定基发展速度与环比发展速度之间的关系
①定基发展速度等于相应时期内各环比发展速度的连乘积。
②两个相邻时期定基发展速度的比率等于相应时期的环比发展速度。
(二)增长速度

【提示】环比增长速度=环比发展速度-1。
3.定基增长速度与环比增长速度不能像定基发展速度与环比发展速度那样互相推算。
4.定基增长速度与环比增长速度之间的推算,必须通过定基发展速度与环比发展速度才能进行。
(一)平均发展速度——采用几何平均法。
(二)平均增长速度
1.平均增长速度既不能由各期的环比增长速度求得,也不能根据一定时期的总增长速度计算。
2.计算思路
(1)平均增长速度是通过它与平均发展速度之间的数量关系求得的。
(2)平均增长速度=平均发展速度-1。
1.“增长1%的绝对值”是进行这一分析的指标。它反映同样的增长速度,在不同时间条件下所包含的绝对水平。
2.计算公式

想要下载本文内容的同学,点击下载按钮,即可免费下载PDF版本。

