本章每年考试分值在2分左右。

学习要求：

①理解回归模型、回归方程、回归系数

②掌握最小二乘法的原理和估计方法，根据估计的回归方程进行回归系数分析

③掌握决定系数以及回归模型的检验。

考点1：回归分析的概念

1、回归分析：指根据相关关系的具体形态，选择一个合适的数学模型，来近似地表达变量间的依赖关系。

2、回归分析和相关分析的关系

联系：

（1）它们不仅具有共同的研究对象，而且在具体应用时，常常必须互相补充。

（2）相关分析需要依靠回归分析来表明现象数量相关的具体形式，而回归分析则需要依靠相关分析来表明现象数量变化的相关程度。

（3）只有当变量之间存在着高度相关时，进行回归分析寻求其相关的具体形式才有意义。

区别：

（2）回归分析：研究变量之间相互关系的具体形式，对具有相关关系的变量之间的数量联系进行测定，确定一个相关的数学方程式，根据这个数学方程式可以从已知量来推测未知量，从而为估算和预测提供了一个重要方法。

（1）相关分析：

①研究变量之间相关的方向和相关的程度。

②相关分析不能指出变量间相互关系的具体形式，也无法从一个变量的变化来推测另一个变量的变化情况。

3、因变量：被预测或被解释的变量，一般用Y表示

4、自变量：用来预测或解释因变量的变量，一般用X表示。

【2023年真题·多选题】用于研究人均收入与人均消费的具体形式的指标是（）。

A. 相关分析

B. 回归分析

C. 偏态分析

D. 描述分析

考点2：最小二乘法

1、估计回归方程：

2、原理：最小二乘法就是使得因变量的观测值yi与估计值ŷi，之间的离差（又称残差）平方和最小来估计参数β0，和 β1，的方法。

根据最小二乘法，使得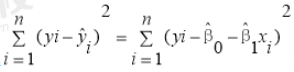最小，可得：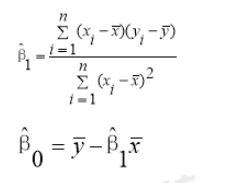

【2023年真题·单选题】在回归分析中常用的估计方法是( )。

A. 最大二乘法

B. 最小二乘法

C. 有效估计法

D. 无偏估计法                          

考点3：一元线性回归模型

根据自变量的多少分为：一元回归模型和多元回归模型。

根据是否是线性分为：线性回归模型和非线性回归模型。

1、一元线性回归模型：描述两个变量之间相关关系的最简单的回归模型。回归模型可以用描述因变量Y如何依赖自变量X和误差项ε的方程来表示。

2、只涉及一个自变量的一元线性回归模型可以表示为：Y=β0+β1X+ε

β0、β1——模型的参数。

（1）Y是X的线性函数（β0+β1X）加上误差项ε。

（2）β0+β1X反映了由于X的变化而引起的Y的线性变化。

（3）误差项ε是个随机变量，反映了除X和Y之间的线性关系之外的随机因素对Y的影响，是不能由X和Y之间的线性关系所解释的Y的变异性。

3、描述因变量Y的期望E（Y）如何依赖自变量X的方程称为回归方程。一元线性回归方程的形式为：

E（Y）=β0+β1X

一元线性回归方程的图示是一条直线，β0是回归直线的截距，β1是回归直线的斜率，表示X每变动一个单位时，E（Y）的变动量。

【2023年真题·多选题】以Y为因变量、X为自变量，建立一元线性回归模型Y=β0+β1X+ε。关于该回归模型的说法()。

A. β0是因变量Y的均值

B. β1是回归直线的斜率

C. ε是不能由X和Y的线性关系所解释的Y的变异性

D. β1表示X每变动一个单位时Y的平均变动量

E. ε是随机变量