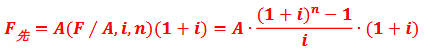1、学习第九章,第一个要点首先学习基本常识,货币时间价值的含义 :
例如:
①20年前在城市中心买个房子,今天如果拍卖,能上千或过亿;
②如果存入银行100元(本金),在约定利率10%的情况下,一年后就是110元(本利和),其中的差额10元钱,就是100元本金在这一年期间的时间价值。
结论:需要经过时间的推移,货币才会实现自我增值。
比如存入银行的这100元,约定利率10%(无风险,无通货膨胀),一年后从银行可获得110元,货币时间价值则可以表示为10元(绝对金额)或增值10%(相对比例)。
这此例子说明的是“资金的时间价值”,是指货币随着时间的推移而发生的增值。
2、第二个基本常识:【简单了解】
①单利,就是指本金来计算。
②复利,就是指本金+利息,再利滚利来计算。
3、一次性收付款项的复利终值与现值
(1)先了解下什么是一次性收付款项:
是指在某一特定时间点上一次性支付(或收取),经过一段时间后再相应地一次性收取(或支付)的款项。
例如:某公司向银行一次性借款50万元,期限为3年,3年后一次性偿还本金和利息。
一次性收付款项主要记两个公式:
①复利终值:F=P(1+i)n 即终值=现值×(1+利率)n
式中:F:终值;P:现值;i:利率;n:计息周期数。(1+i)n称为复利终值系数,记为(F/P,i,n),可通过查复利终值系数表获得。【括号里面,F是终值,斜杠往后的参数(P,i,n)是已知,是要“求”F终值。】
②复利现值:P=F(1+i)-n 即 现值=终值×(1+利率)-n
式中字母同上。
【注意】终值与现值注意时间节点:现值看头,终值看尾,头和尾都是指时间节点(概念中讲的“某一时点上”),根据出题情况来判断。
4、什么是年金?
年金是指每隔一定相等时间,收到或支付的相同数量的系列款项。
判断标准:相等时间、相同数量即等时等量,每期发生(间隔期不一定是一年)。
比如60岁退休的的人,每月月末都会收到养老金2000元,这2000元就可称为年金。
年金按其每次收付发生的时点不同,可分为后付年金,先付年金,递延年金,永续年金等几种。如下图

对于这几个年金,我们可以这么理解:
①等额支付贷款,为后付年金,且是后付年金现值形式;
②生活中比较常见的先付款才能使用的如水电煤气,这种是典型的是先付年金形式;
③保险公司投保人先缴费一定的期间(累积期),再由保险公司在一定期间或投保人退休后开始给付年金(清偿期),这是递延年金形式。
④优先股无到期日,可视为永续年金。
5、年金的终值与现值【难点重点掌握】
年金类型 | 终值(F) | 现值(P) |
后付年金 |
|
|
先付年金 | F=后付年金终值×(1+i) | P=后付年金现值×(1+i) |
递延年金 | 指指在最初若干期没有收付款项,后面若干期才有等额收付的年金形式。 | P=A[(P/A,i,n)](1+i)-m, A是第几年流入金额。 |
永续年金 | 指无限期收付的年金。一般优先股因为有固定的股利而无到期日,因此优先股股利有时可视为永续年金。 | P=A/i,举例:某优先股,每年股息2元,利率(或投资者要求的必要报酬率)为每年6%,则该优先股的现值为2/6%=33.33(元)。 |
【注意:表格中年金的重点学习后付年金终值与现值,先付年金终值与现值。递延年金本身难度最大,在工商教材上不作重点讲解,教材也只是大概讲了一下。永续年金比较简单,记住公式。】
下面重点介绍两种方法:
(1)后付年金的终值与现值:
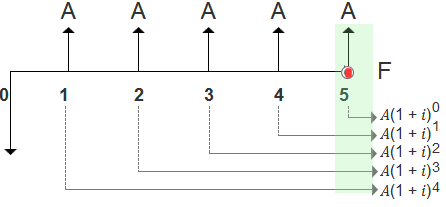
①后付年金终值: | 是一定时期内每期期末等额的系列收付款项的复利终值之和。 |
图示 |
图示意思表达的是: 第5年年末,支付年金A的终值:F5=A(1+i)0; 依此类推: 第1年年末,支付年金A的终值:F1=A(1+i)4; 将这5年的公式相加,就得到如下方法一公式: |
方法一: |
|
方法二: |
|
②后付年金现值: | 指一定时期内每期期末等额的系列收付款项的复利现值之和。 |
图示: |
图示意思表达的是: 第1年年末,支付年金A的现值:P1=A(1+i)-1; 依此类推: 第5年年末,支付年金A的现值:P5=A(1+i)-5; 将这5年的公式相加,就得到如下方法一公式: |
方法一: |
|
方法二: |
|
(2)先付年金的终值与现值:
①先付年金终值: | 由于先付年金与后付年金付款时间不同,n期先付年金终值比n期后付年金的终值多计算一期利息。所以,先付年金终值=后付年金终值×(1+利率)。公式为:F=A×(F/A,i,n)×(1+i) 意思是: 在 n 期后付年金终值基础上乘上(1+i)就是 n 期先付年金终值,即在后付年金终值系数的基础上乘上(1+i)就是 n 期先付年金的终值。先付年金的终值计算公式为: |
②先付年金现值: | 由于先付年金与后付年金付款时间不同,n期先付年金现值比n期后付年金的现值少折现一期。所以,先付年金现值=后付年金现值×(1+利率); 公式为:P=A×(P/A,i,n)×(1+i)。 意思是: n 期先付年金比 n 期后付年金少折现一期,因此在 n 期后付年金现值的基础上乘以(1+i),便可求出 n 期先付年金的现值。其计算公式为: |
1.【2021真题 · 单选】关于n 期先付年金与 n 期后付年金的说法,正确的是( )。
A.n 期先付年金现值比 n 期后付年金现值多折现 2 期
B.n 期先付年金现值比 n 期后付年金现值少折现 1 期
C.n 期先付年金现值比 n 期后付年金现值少折现 2 期
D.n 期先付年金现值比 n 期后付年金现值多折现 1 期
n 期先付年金现值比 n 期后付年金现值少折现 1 期。选项 B 正确。
备考2023年中级经济师可以参考参考中级经济师考试【工商管理】章节题,多多练习,才能对知识点记忆深刻。

温馨提示:文章由作者233网校-lxh独立创作完成,未经著作权人同意禁止转载。
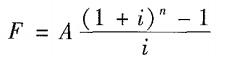
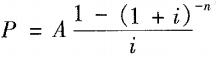
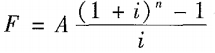 【直接用公式求,将值代入进来。】
【直接用公式求,将值代入进来。】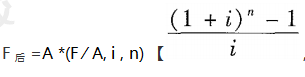 ,称为年金终值系数,记为(F ∕ A, i , n) ,通过系数表查得系数。】
,称为年金终值系数,记为(F ∕ A, i , n) ,通过系数表查得系数。】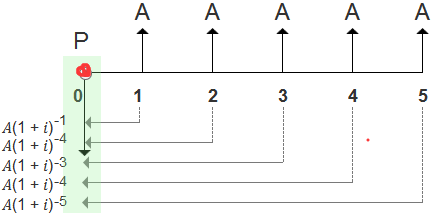
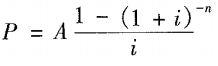 【方法同上。】
【方法同上。】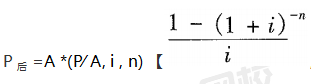 ,称为年金终值系数,记为(P∕ A, i , n) ,通过系数表查得系数。】
,称为年金终值系数,记为(P∕ A, i , n) ,通过系数表查得系数。】