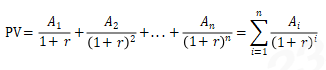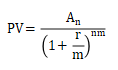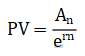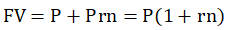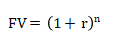考点一:利率的计算
利率:指借款人在单位时间内应支付的利息与借贷资金的比率。
按利率的决定方式不同:固定利率与浮动利率
按利率的真实水平不同:名义利率与实际利率。 实际利率=名义利率-通货膨胀率
按计算利率的期限单位不同:年利率、月利率、日利率
年利率=月利率×12=日利率×360
考点二:单利与复利
单利 | 复利 | 连续复利 | |
含义 | 指不论借贷期限的长短,仅按本金计算利息,上期本金产生的利息不计入下期本金计算利息。 | 也称利滚利,是将每一期产生的利息加入本金一并计算下一期的利息。 | 如果m→∞,则(1+r/m)mn趋于ern,,其中e为自然对数的底,约等于2.71828。 |
计算公式 | I=Prn I:利息,P:本金, r:利率,n:计息期数
| FV=P(1+r)n I=FV-P=P[(1+r)n-1] FV:本息和,I:利息, P:本金,r:利率,n:计息期数 若本金为P,年利息为r,每年的计息次数为m,则第n年末的本息和为 FVn=P(1+r/m)mn | 对于本金以连续复利计算第n年年末的本息和:FVn=Pern |
每年的利息次数越多,最终的本息和越大。随着计算间隔的缩短,本息和以递减的速度增加,最后等于连续复利的本息和。 | |||
记忆小tips:单利只有乘法,复利是乘方,连续复利是e的乘方(考试的时候可以合理利用计算器)
考点三:现值与终值
现值 | 终值 | |||
含义 | 又称在用价值,是现值和将来(或过去)的一笔支付或支付流在今天的价值。 | 又称将来值或本息和现在一定量的资金在未来某一时点上的价值、 决定因素:现值的大小,利率的高低,借款期限和计息方式。 | ||
类型 | 系列现金流的现值 | 连续复利下的现值 | 单利 | 复利 |
计算公式 |
PV:现值,Ai:i年年末的现金流量,r:贴现率 |
An:第n年年末的现金流量, r:年贴现率, m:年计息次数 如果连续复利, 则m→无穷大 | 年利率为r ,n年后的终值
|
其中(1+r)n为复利终值系数 |
每年的计息次数越多,现值越小。随着计息间隔的缩短,现值以递减的速度减小,最后等于连续复利条件下的现值。 | ||||
记忆小tips:现值是除,终值是乘;系列现金流的现值是将每个系列的现金流贴现到当时的时间点再相加。
经典考题:
1、假定某投资者用10000元进行投资,已知年利率为8%,按复利每半年计算一次利息,则1年后该投资者的本息和为( )元。
A、10400
B、10800
C、10816
D、11664
2、假定年贴现率为6%,2年后一笔10000元的资金的现值为( )元。
A、8900
B、8920
C、9100
D、9750
温馨提示:文章由作者233网校-py独立创作完成,未经著作权人同意禁止转载。