【备考点拨】许多考生反馈说回归分析这一章看不懂，牵涉到许多模型、公式问题，比较难以理解，但是从历年考试来看，本章节的知识点考查方式都比较稳定，考点的可预测性较强，考点后小编精选了历年的真题帮助大家理解考点，大家注意要利用好，学会举一反三。
本章主要掌握回归分析、回归模型的含义、最小二乘法的原理（注意公式需要记忆），以及决定系数的含义。赵聪老师15分钟就把这章节内容讲得清晰明了，详情可戳>>>
考点一：回归分析
1、回归分析：指根据相关关系的具体形态，选择一个合适的数学模型，近似地表达变量间的依赖关系。
2、回归分析和相关分析
相关分析 | 回归分析 | |
联系 | 不仅具有共同的研究对象，而且在具体应用时，常常必须互相补充。 | |
区别 | 1、研究变量之间相关的方向和相关的程度。 2、不能指出变量间相互关系的具体形式，也无法从一个变量的变化来推测另一个变量的变化情况。
| 1、研究变量之间相互关系的具体形式。 2、对具有相关关系的变量之间的数量联系进行测定，确定一个相关的数学方程式，根据这个数学方程式可以从已知量来推测未知量，从而为估算和预测提供了一个重要的方法。 因变量：被预测或被解释的变量 自变量：用来预测或解释因变量的变量 |
经典真题：
1、关于相关分析和回归分析的说法正确的有（ ）。
A、相关分析可以从一个变量的变化来推测另一个变量的变化
B、相关分析和回归分析中都需要确定因变量和自变量
C、当变量之间存在着相关性时进行回归分析
D、相关分析需要依靠回归分析来表明现象数量相关的具体
E、相关分析与回归分析之间在研究目的和方法上是不同的
考点二：回归模型
1、回归模型的分类
分类依据 | 类别 |
自变量的多少 | 一元回归模型、多元回归模型 |
回归模型是否线性 | 线性回归、非线性回归 |
2、一元线性回归模型：Y＝β0＋β1X＋ε
β0、β1：模型参数
β0＋β1X：反映由自变量X的变化引起的因变量Y的线性变化。
误差项ε：随机变量，表示除X和Y的线性关系之外的随机因素对Y的影响，是不能由X和Y的线性关系所解释的Y的变异性。
经典真题：
1、一元线性回归模型Y=β0+β1X+ε中反映除自变量之外的随机因素对因变量的影响是（ ）
A、ε
B、β0
C、β0+β1X
D、β1
考点三：最小二乘法
1、最小二乘法：指使因变量的观测值与估计值间的离差（又称残差）平方和最小来估计参数的方法。
根据最小二乘法，使得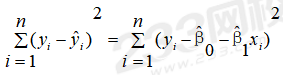
最小，可得：
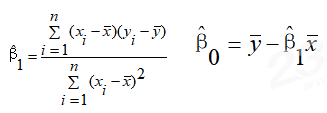
考点四：回归模型的拟合效果分析
1、决定系数R2：也称为拟合优度或判定系数，可以测度回归模型对样本数据的拟合程度。
取值范围：[0，1]
R2＝0，回归直线无法解释因变量变化，因变量与自变量无关。
R2＝1，回归直线可解释因变量的所有变化。
R2越高，拟合效果越好，即模型解释因变量的能力越强。
经典真题：
1、在某城市随机抽取1000户居民作为样本对该城市居民消费水平进行研究，对居民月消费支出Y（单位：元）和月收入X（单位：元），建立回归模型，得到估计的回归系数Y＝1300＋0.6X，决定系数0.96，关于该模型的说法正确的有（ ）。
A、居民月收入和月消费支出之间正相关
B、回归模型的拟合效果很好
C、居民月收入难以解释月消费支出的变化
D、居民月收入每增长1元，月消费支出将平均增长0.6元
E、居民月收入为10000元时，居民人均月消费支出大约为7300元
温馨提示：文章由作者233网校-py独立创作完成，未经著作权人同意禁止转载。
