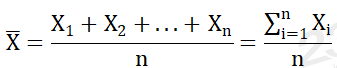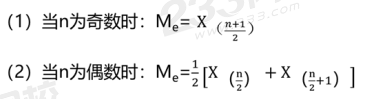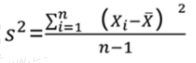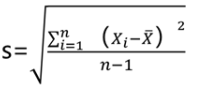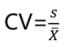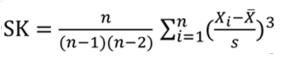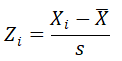领取完整版计算公式>>

中级经济基础第二十四章 描述统计
1.均值 | 均值也叫平均数,就是数据组中所有数值的总和除以该组数值的个数。 设一组数据为X1,X2,...,Xn,平均数为
|
2.中位数——先排序再找中间位置 | 定义:把一组数据按从小到大或从大到小的顺序进行排列,位置居中的数值叫作中位数,用Me表示;中位数将数据分为两部分,其中一半数据小于中位数,另一半数据大于中位数。 计算公式:设一组数据为X1,X2,…,Xn,按从小到大顺序为X(1),X(2),…,X(n),则中位数为:
|
【例题】2016年某企业集团下辖8个分公司的销售额分别为8000万元、800万元、200万元、600万元、3000万元、2800万元、2200万元、5000万,这组数据的中位数是( )万元。
A.2200
B.2800
C.2500
D.3000
1.方差 | 定义:方差是数据组中各数值与其均值离差平方的平均数。 特征:能较好地反映出数据的离散程度,是实际中应用最广泛的离散程度测度值。 结论:方差越小,说明数据值与均值的平均距离越小,均值的代表性越好。 计算公式: (1)对于总体数据(N)为总体规模:
(2)对于样本数据(n为样本规模): (3)结论 ①在有放回的简单随机抽样中,样本方差s2是总体方差σ2 的无偏估计量; |
2.标准差 | 1.定义 (1)方差是反映数据离散程度的重要测度指标,但是其单位是原数据单位的平方,没有解释意义。 (2)我们经常使用标准差来测度数据的离散程度,标准差即方差的平方根。 2.计算公式对于样本数据,常用的标准差计算公式为: |
3.离散系数 | 1.定义:离散系数也称变异系数或标准差系数,即标准差与均值的比值,主要用于不同类别数据离散程度的比较,记为CV。 2.计算公式 : |
1.偏态系数
| 1.定义: (1)偏度是指数据分布的偏斜方向和程度,描述的是数据分布对称程度。 2.计算公式
结论: (1)SK=0:数据分布是对称的; (2)SK>0:数据分布右偏;0~ 0.5(轻度)、0.5~ 1(中度)、大于1(严重) (3)SK<0:数据分布右左;0~- 0.5(轻度)、-0.5~ -1(中度)、大于- 1(严重) |
2.标准分数 | 计算公式:标准分数=(数值-均值)÷标准差,符号如下:
结论: (1)标准分数也称为Z分数,是统计上常用的一种标准化方法。 |
【例题】(2018年)将数值减去均值所得的差除以标准差,所得的统计量为( )。
A.相关系数
B.标准分数
C.方差
D.偏态系数
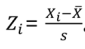
【例题】(2019年)关于偏态系数的说法,正确的是( )。
A、偏态系数为正值,说明数据对称
B、偏态系数的绝对值越大,说明数据越对称
C、偏态系数等于0,说明数据对称
D、偏态系数等于1,说明数据对称
【例题】(2020年)如果一组数据的偏态系数为0.3,则该组数据的分布为( )
A、轻度右偏
B、轻度左偏
C、中度左偏
D、中度右偏
温馨提示:文章由作者233网校-lxh独立创作完成,未经著作权人同意禁止转载。
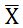 的计算公式:
的计算公式: