考点二 资金时间价值的计算
(一)单利和复利
1.单利
概念:单利利息和时间成线性关系,只计算本金的利息,本金所产生的利息不再计算利息。
计算公式:I=P·n·i
式中,I是利息额;P是本金;i是利率;n是计息周期。
2.复利
概念:复利指每期末不支付利息,而将该期利息转为下期的本金,即不但本金产生利息,而且利息也产生利息(即利滚利)。
计算公式:F=P×(1+i)n,I=F-P
式中,I是利息额;F是本利和(还本付息总额);P是本金;i是利率;n是计息周期。
【注意】单利没有完全地反映出资金运动的规律性,不符合资金时间价值的本质,因而通常采用复利计算。
【例2·单选题】将1000元存入银行,年利率为6%,如果按单利计算,则三年后的本利和为( )元。
A.1180
B.1191.02
C.1080
D.1000
【答案】A
【解析】利息=1000×6%×3=180(元),本利和=looo+1000×6%×3=1180(元)。
【例3·单选题】将l000元存入银行,年利率为6%,如果按复利计算.则三年后的本利和为( )元。
A.1180
B.11 91.O2
C.1080
D.1000
【答案】B
【解析】本利和=1000×(1+6%)3=1191.02(元)。
【注意】本金与利率均相同时,按复利计算的利息要比按单利计算的利息高,这是由于利息的部分也产生利息的缘故。
(二)现金流量图
现金流量图
概念 |
用图示的方法将现金的流进与流出、量值的大小、发生的时点描绘出来,将该图称为现金流量图 |
|
画法
|
①一条向右的带箭头的线代表时间轴 |
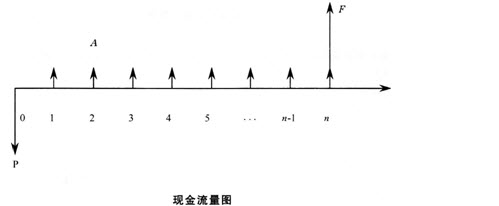
【注意】
(1)流入和流出是相对而言的,借方的流入是贷方的流出,反之亦然;
(2)现金流量图是后续计算的重要基础。需要熟练掌握。
(三)资金时间价值的计算
资金时间价值的计算
|
三个值 |
①P:现值:表示现在时点的资金额 |
|
两个因素 |
①利率(i).②计息期(n) |
|
六种换算
|
①P~F,已知现值,换算为终值 |
【注意】因数表示为(A/P,i,n)的含义:
A/P表示经济活动的内涵,斜杠右边的表示已知的值.斜杠左边的表示要求的值。如A/P表示已知现值P求年值A;i和n表示两个因素:利率和计息期。
1.现值换算为终值P~F
F=P(1+i)n
形象记忆:(存款)一次存钱,到期本利合计多少。
系数名称:一次支付复本利和因数(F/7P,i,n)。
【例4·单选题】某建筑商向金融机构贷款500万元,按复利计息,年利率为12%。若第5年末一次还本付息,应偿还( )万元。
A.687
B.881
C.965
D.600

形象记忆:(存款)已知到期本利合计数,求最初本金。
系数名称:一次支付现值因数(P/F,i,n)。
【例5·单选题】将一笔资金按年利率6%存入银行,以复利计息,要在5年后本利和为l00万元,则现在应存款( )万元。
A.60
B.74.73
C.65.25
D.55.65
【答案】B
【解析】本题考查终值换算为现值(F~P)的计算。P—F(P/F,i,n)=F/(1+i)n=100÷(1+6%)5=74.73(万元)。
3.年值换算为终值A~F
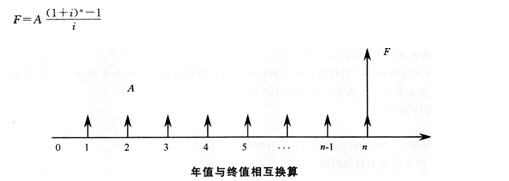
形象记忆:(存款)等额零存整取。
系数名称:等额支付将来值(终值)因数(F/A,i,n)。
【例6·单选题】若每年年末存入银行10万元,年利率为6%,则5年后的复本利和为( )万元。已知(F/A,i,n)=5.637。
A.56.37
B.75.25
C.54.25
D.60.65
【答案】A
【解析】本题考查年值换算为终值(A~F)的计算。F=A(F/A,i,n)=10×5.637=56.37(万元)。
4.终值换算为年值F~A

形象记忆:(存款、养老保险)已知最后要取出一笔钱,每年应等额存人多少钱。年轻时定期等额支付养老金,到一定年龄一次性取出,问一次性可取多少钱。
系数名称:等额支付偿债基金因数(A/F,i,n)。
【例7·单选题】某设备估计尚可使用5年。为此准备5年后进行设备更新,所需资金估计为30万元,若存款利率为5%,从现在开始每期末均等的存款,则应存款( )万元。已知(A/F,5%,5)=0.18097。
A.6.426
B.5.429
C.4.846
D.5.868
【答案】B
【解析】本题考查终值换算为年值(F~A)的计算。A=F(A/F,i,n)=30×(A/F,5%,5)=30X0.18097=5.429(万元)。
5年值换算为现值A~P

形象记忆:(按揭)住房按揭贷款。已知贷款额,求月供或年供。
系数名称:资本回收因数(A/P,I,n)。
【例8·单选题】某人贷款12万元,分l0年摊还,年利率为6%,按月计息,则每月的偿还金额为( )元。
A.1332
B.1532
C.1254
D.1554
【答案】A
【解析】本题考查现值换算为年值(P~A)的计算。本题需要注意的是计息期。已知的是年利率,但求的是月还款额,P=12万元,因此i=6%÷l2=0.5%,n=10 × 12=120。所以A=P(A/P,6%/12,120)=12× 0.0111=0.1332(万元)。
资金的时间价值换算总结
换算 |
系数名称 |
公式 |
形象记忆 |
|
现值换算为终值 |
一次支付复本利和因数(F/P,i,n) |
F=P(F/P,i,n) |
(存款) |
|
终值换算为现值 |
一次支付现值因数(P/F,i.n) |
P=F(P/F,i,n) |
(存款) |
|
年值换算为终值 |
等额支付终值因数(F/A,i,n) |
F—A(F/A,i,n) |
(存款)等额零存整取 |
|
终值换算为年值 |
等额支付偿债基金因数(A/F,i,n) |
A=F(A/F,i,n) |
(存款) |
|
年值换算为现值
|
等额支付现值因数(P/A.i,n)
|
P=A(P/A,i,n)
|
(养老金) 年可领取年金若干,求当初存入多少钱 |
|
现值换算为年值 |
资本回收因数(A/P,i,n) |
A=P(A/P,i,n) |
(按揭)(养老金) |
(四)资金时间价值换算的基本公式推导的假定条件
为了准确地运用前面的六个公式,必须搞清其推导的前提条件,当所遇到的问题的现金流量不符合上述公式推导的前提条件时,只要将其折算成符合上述假设条件后。即可运用上述的基本公式。这些条件是:
1.实施方案的初期投资假定发生在方案的寿命期初

2.方案实施中发生的经常性收益和费用假定发生在计息期的期末
(1)事实上现金流在一年中随机地发生,但是公式默认为现金流发生在每一期的期末。而且在题目中如没有特别说明,都假设现金流发生在期末,即每年的年末。
(2)1年上的现金流假设发生在第1年年末,N年上的现金流假设发生在第N年年末。
(3)现金流量图中的0点,表示第1年的年初,其他年数1、2、3、…、N都表示是这一年的年末。
(4)只有初始投资是在第一个计息期的期初,其他年内的投入或支出,都要归在这一个计息期的期末。
3.本期的期末为下期的期初
前一期的期末就意味着今期的期初,除了第一个计息期外,一笔收入或支出如果发生在这一年的年初,则在现金流量图中必须表示为上一年的流入或流出中。
【例9·单选题】某建设项目,建设期为3年,建设期第1年贷款400万元,第2年贷款500万元,第3年贷款300万元,贷款均为年初发放,年利率为l2%,采用复利法计算建设期的贷款利息,则第3年末贷款的复本利和为( )万元。
A.1525.16
B.1375.17
C.1489.17
D.1625.17
【答案】A
【解析】注意本题中的特殊条件“贷款均为年初发放”。
F=P1(F/P,12%,3)+P2(F/P,12%,2)+P3(F/P,12%,1)=400 × 1.4049+500×1.2544+300×1.12=1525.16(万元)。

6.年值A是在考察期间间隔发生的;当问题包括P和A时,系列的第一个A是在P发生一个期间后的期末发生的;当问题包括F和A时,系列的最后一个A与F同时发生。
(1)当包括P和A时,系列的第一个A在P发生一个期间后的期末发生。


【例10·单选题】为了在未来5年内通过储蓄得到3万元,若利率为12%,每年年初应存入( )元。
(P/F,12%,1)=0.8929,(A/F,12%,5)=0.1574。
A.3816
B.4516
C.4216
D.5216
【答案】C
【解析】

【注意】
(1)第1年年初在零的位置上;
(2)第1次A换算为F,在第4年的位置上,不在第5年位置,所以必须再进行一次换算。
A=F(P/F,i,n2)(A/F,i,n1)=30000×(P/F,12%,1)×(A/F,12%,5)=4216(万元)。
(五)三值(年值、现值、终值)之间换算题型汇总
1.常见题型
(1)在三个值之间进行直接的换算(初级——直接套公式)。
(2)条件不符合公式的假定条件,需进行一定的变换(中级——套用多个公式换算)。
(3)综合题,主要是案例分析题,结合运用各知识,需要对题目有一个非常透彻的理解(高级)。
2.解题步骤
第一步,审题。复杂题必须画出现金流量图帮助理解。
第二步,确定换算关系。审题后确定其经济活动的内涵是哪两个值之间的换算,写出关系式,如A=P(A/P,i,n),这需要熟练掌握六种换算。
第三步,审查条件。题中的条件与公式换算的假定条件是否一致,如不一致,则需调整换算关系式。
第四步,检查一致性。注意i与n的内涵是否一致。
(1)如果i是年(季、月)利率,则n就是以年(季、月)为标准的计息期。
(2)如果没有明确告知,则季利率等于年利率除以4,月利率等于年利率除以12。
第五步,计算。将已知数据带入关系式中计算。
【例11·单选题】某人每年年末存款1000元,前8年年利率为3%,后2年的年利率变为4%,问该人存款的10年末复本利和为( )元。已知(F/A,3%.8)=8.8932,(F/P,4%,2)=1.082,(F/A,
4%,2)=2.040。
A.11662
B.11562
C.12562
D.12662
【答案】A
【解析】第一步,审题。先画出现金流量图。

第二步,确定换算关系A~F。本题分两部分分别计算相加。
第三步,审查条件。
■每年年末,符合公式;
■当包括F和A时,系列的最后一个A与F同时发生,也就是两部分折算成F。和F。时,分别处在第8年和第10年的位置上;
■两部分换算后的终值不在同一时点上,不能直接进行代数运算,必须再进行一次换算。将发生在第8年的F。再换算到第l0年的位置上,他们之间的关系相当于P~F;
■调整后的公式为:
F=A1(F/A,3%,8)(F/P,4%,2)+A2(F/A,4%,2)。
第四步,注意一致性。
■年利率与计息期一致;
●注意第二次折算时,采用最新的利率。
第五步,计算。复本利和=1000×8.8932×1.08+1000×2.040=11662(元)。
【例l2·单选题】欲进行房地产开发,需购置土地.假设土地价款支付方式是:现时点支付600万元,此后,第一个5年每半年支付40万元;第二个5年每半年支付60万元;第三个5年每半年支付80万元;
按复利计算,每半年的资本利率为4%。则该土地的价格相当于现时点的值是( )万元。
A.1549.35
B.16562.25
C.15562.75
D.14662.35
【答案】A
【解析】作法一:
P=600+[40×(F/A,4%,30)+20×(F/A,4%,20)+20×(F/A,4%10)]×(P/F,4%,30)=600+[40×56.085+20×29.778+20×12.006]×0.3083=1 549.28(万元)。
【注意】方法不同所得结果稍有误差,但是并不影响考生对答案作出判断。

































