
抽样误差虽然无法避免,但可以计算。
以不放回简单随机抽样下均值估计量为例:
假设从总体的N个单元中按照不放回简单随机抽样方法抽取n个单元作为样本,用Y1,Y2,...,YN表示总体关于变量Y的N个观测值,用y1,y2,...,yn表示样本中的n个观测值。则估计量![]() 的方差为:
的方差为:
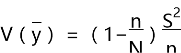 其中,
其中,![]() 为总体方差
为总体方差
(1)抽样误差与总体分布有关,总体单位值之间差异越大,则总体方差S2越大,抽样误差就越大。
(2)抽样误差与样本量n有关,在其他条件相同情况下,样本量越大,抽样误差就越小。
(3)抽样误差与抽样方式和估计量的选择也有关系。 例如,分层抽样的估计量方差一般小于简单随机抽样。
(4)利用有效辅助信息也可以有效地减小抽样误差。
实践中,总体方差S2是未知的,可以利用样本方差来估计,因此估计量方差的估计公式为:
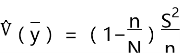 其中,
其中,![]() 为总体方差
为总体方差




































