估计量的性质
估计量的性质相关课程
 估计量的性质考点解析
估计量的性质考点解析
 估计量的性质介绍
估计量的性质介绍
1、估计量的无偏性:对于不放回简单随机抽样,所有可能的样本均值取值的平均值总是等于总体均值,这就是样本均值估计量的无偏性。
2、估计量的有效性:由于方差是度量分布密集或离散状况的重要指标,估计量方差常用于描述抽样误差。估计量方差越大,说明可能的样本估计值之间的差异越大,用样本统计量估计总体参数的效率就越低,抽样误差越大。
3、估计量的一致性:随着样本量的增大,估计量的值如果稳定于总体参数的真值,这个估计量就有一致性,可称为一致估计量。

估计量的无偏性怎么理解?

估计量的有效性怎么理解?

估计量的一致性怎么理解?

抽样误差的估计公式是什么?

样本量的影响因素是什么?
估计量的性质考点试题
大咖讲解:估计量的性质

抽样误差的估计
抽样误差虽然无法避免,但可以计算。
以不放回简单随机抽样下均值估计量为例:
假设从总体的N个单元中按照不放回简单随机抽样方法抽取n个单元作为样本,用Y1,Y2,...,YN表示总体关于变量Y的N个观测值,用y1,y2,...,yn表示样本中的n个观测值。则估计量![]() 的方差为:
的方差为:
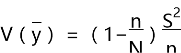
其中,![]() 为总体方差
为总体方差
(1)抽样误差与总体分布有关,总体单位值之间差异越大,则总体方差S2越大,抽样误差就越大。
(2)抽样误差与样本量n有关,在其他条件相同情况下,样本量越大,抽样误差就越小。
(3)抽样误差与抽样方式和估计量的选择也有关系。 例如,分层抽样的估计量方差一般小于简单随机抽样。
(4)利用有效辅助信息也可以有效地减小抽样误差。
实践中,总体方差S2是未知的,可以利用样本方差来估计,因此估计量方差的估计公式为:
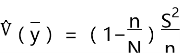
其中,![]() 为总体方差
为总体方差

样本量的计算
1、样本量的影响因素:
(1)调查的精度(同向).调查的精度是指用样本数据对总体进行估计时可以接受的误差水平。要求的调查精度越高(误差水平越小),所需要的样本量就越大。
(2)总体的离散程度(同向):在其他条件相同情况下,总体方差越大,所需要的样本量也越大。
(3)总体的规模:对于大规模的总体,总体规模对样本量的需求几乎没有影响。对小规模的总体,总体规模越大,为保证相同估计精度,样本量也要随之增大(但不是同比例的)。
(4)无回答情况:若无回答率较高,样本量要大一些。
(5)经费的制约:样本量是调查经费与调查精度之间的某种折中和平衡。
(6)调查的限定时间及实施调查的人力资源。

估计量的无偏性
估计量的无偏性:对于不放回简单随机抽样,所有可能的样本均值取值的平均值总是等于总体均值,这就是样本均值估计量的无偏性。

估计量的有效性
估计量的有效性:由于方差是度量分布密集或离散状况的重要指标,估计量方差常用于描述抽样误差。估计量方差越大,说明可能的样本估计值之间的差异越大,用样本统计量估计总体参数的效率就越低,抽样误差越大。

估计量的一致性
估计量的一致性:随着样本量的增大,估计量的值如果稳定于总体参数的真值,这个估计量就有一致性,可称为一致估计量。
相关知识点pdf资料

划重点!2024年中级经济师经济基础第十四章核心考点梳理

2024年中级经济师《经济基础》经典母题汇总:第一章

年年考!2024年中级经济师经济基础第六章核心考点梳理!

考核12分!2024年中级经济师经济基础第八章核心考点梳理!

曾出7道考题!2024年中级经济师经济基础第七章核心考点梳理!

曾考核10题!2024年中级经济师经济基础第九章核心考点梳理

反复考!2024年中级经济师经济基础第十章核心考点梳理

2024年中级经济师《经济基础》经典母题汇总:第四章

2024年中级经济师《经济基础》经典母题汇总:第三章

2024年中级经济师《经济基础》经典母题汇总:第五章

重点掌握这3点!2024年中级经济师经济基础第十一章核心考点梳理

出题19分!2024年中级经济师经济基础第十二章核心考点梳理

分值占比高!2024年中级经济师经济基础第十三章核心考点梳理

2024年中级经济师《经济基础》经典母题汇总:第二章

2024年中级经济师《经济基础》经典母题汇总:第六章

2024年中级经济师《经济基础》经典母题汇总:第七章

2024年中级经济师《经济基础》经典母题汇总:第八章

重点记忆!2024年中级经济师经济基础第十五章核心考点梳理

收藏!2024年中级经济师经济基础第十六章核心考点梳理

重点掌握!2024年中级经济师经济基础第十七章核心考点梳理

每年考核5-10分!2024年中级经济师经济基础第十八章核心考点梳理

重点就这些!2024年中级经济师经济基础第十九章核心考点梳理

考核4-7分!2024年中级经济师经济基础第二十章核心考点梳理

马上收藏!2024年中级经济师经济基础第二十一章核心考点梳理

2024年中级经济师《经济基础》经典母题汇总:第九章

2024年中级经济基础考什么?如何备考?一文全面了解

2023年《中级经济基础》第一部分考前必会考点17个汇总

2023年《中级经济基础》第二部分考前必会考点17个汇总

速背!中级经济基础知识记忆口诀32条汇总

考前必看!2023年中级经济基础易混淆考点总结(上)

2023年《中级经济基础》第三部分考前必会考点12个汇总

233网校郑伟老师特供:一文搞定中级经济师经济基础人名理论

考前必看!2023年中级经济基础易混淆考点总结(下)

2023年《中级经济基础》第四部分考前必会考点11个汇总

2023年经济师《中级经济基础》第六部分考前必会考点7个汇总

2023年《中级经济基础》第五部分考前必会考点10个汇总

一文搞定数字考点:2024年中级经济师《经济基础》数字考点总结

划重点!2024中级经济师经济基础第二十二章核心考点梳理

三个半月时间一次通过中级经济师双科,我是这样做的!

二战稳扎稳打,为评职称涨工资拿下中级经济师

经验分享:在职零基础3个月一次性通过中级经济师

纯自学!253分高分一次性通过中级经济师2科

在职备考中级经济师,二战过线,心态平和,方法得当

痛定思痛!总结失败经验,二战改变学习方法,顺遂拿下中级经济师

2024年中级经济基础第一章核心考点,背这些就够!

速收藏!2024年中级经济基础第二章核心考点梳理!

每年必考!2024年中级经济基础第三章核心考点梳理汇总!

考核2-4分,2024年中级经济师经济基础第四章核心考点梳理

2024年中级经济师经济基础第五章核心考点梳理,掌握这三点足够!

2024年中级经济师《经济基础》经典母题汇总:第二十八章

2024年中级经济师《经济基础》经典母题汇总:第十七章

2024年中级经济师《经济基础》经典母题汇总:第十六章

2024年中级经济师《经济基础》经典母题汇总:第十九章

2024年中级经济师《经济基础》经典母题汇总:第十八章

2024年中级经济师《经济基础》经典母题汇总:第二十一章

2024年中级经济师《经济基础》经典母题汇总:第二十章

2024年中级经济师《经济基础》经典母题汇总:第二十三章

2024年中级经济师《经济基础》经典母题汇总:第二十二章

2024年中级经济师《经济基础》经典母题汇总:第二十四章

2024年中级经济师《经济基础》经典母题汇总:第二十五章

2024年中级经济师《经济基础》经典母题汇总:第二十六章

2024年中级经济师《经济基础》经典母题汇总:第二十七章

2024年中级经济师《经济基础》经典母题汇总:第十三章

2024年中级经济师《经济基础》经典母题汇总:第二十九章

2024年中级经济师《经济基础》经典母题汇总:第三十章

2024年中级经济师《经济基础》经典母题汇总:第三十一章

2024年中级经济师《经济基础》经典母题汇总:第三十二章

2024年中级经济师《经济基础》经典母题汇总:第三十三章

2024年中级经济师《经济基础》经典母题汇总:第三十五章

2024年中级经济师《经济基础》经典母题汇总:第三十四章

2024年中级经济师《经济基础》经典母题汇总:第三十七章

2024年中级经济师《经济基础》经典母题汇总:第三十六章

速背!2024年中级经济基础32条速记记忆口诀!

考核重点!2024年中级经济师经济基础教材新增考点18个!

2024年中级经济师《经济基础》经典母题汇总:第十二章

2024年中级经济师《经济基础》经典母题汇总:第十章

重点记忆!2024中级经济师经济基础第二十三章核心考点梳理

郑伟老师直播重点回放!一节课搞定中级经济基础难点——弹性

郑伟老师直播重点回放!2024年中级经济基础新课第二课要点

郑伟老师直播重点回放!中级经济基础第三章曲线考点都在这了!

每年考4-5分!2024中级经济师经济基础第二十四章核心考点梳理

考核3-7分,2024中级经济师经济基础第二十五章核心考点梳理

就掌握这些!2024中级经济师经济基础第二十六章核心考点梳理

爱出计算题!2024中级经济师经济基础第二十七章核心考点梳理

2024年中级经济师《经济基础》经典母题汇总:第十一章

分值占比高!!2024中级经济师经济基础第二十八章核心考点梳理

新增!2024年中级经济基础新增考点考题10道,试试你都能做对吗?

出题3-8分!2024中级经济师经济基础第二十九章核心考点梳理

考核4-6分!2024中级经济师经济基础第三十章核心考点梳理

马上收藏!2024中级经济师经济基础第三十一章核心考点梳理

就学这些!2024中级经济师经济基础第三十二章核心考点梳理

识记!2024中级经济师经济基础第三十三章核心考点梳理

考核6-7分,2024中级经济师经济基础第三十四章核心考点梳理

重点!考核4-7分!2024中级经济师经济基础第三十五章核心考点梳理

考核3-6分!2024中级经济师经济基础第36章核心考点梳理

考核5-7分!2024中级经济师经济基础第37章核心考点梳理

2024年中级经济师《经济基础》经典母题汇总:第十五章


