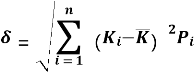风险价值的相关概念
风险价值的相关概念相关课程
风险价值的相关概念考点解析
风险价值的相关概念介绍
1、风险：指由于未来影响因素的不确定性而导致其财务成果的不确定性。
2、风险价值：又称风险收益、风险报酬，是指投资者由于冒着风险进行投资而获得的招过资金时间价值的额外收益。
风险报酬有两种表示方法∶风险报酬额和风险报酬率。
3、投资必要报酬率 =资金时间价值（无风险报酬率）＋ 风险报酬率
（一般情况下，可以将购买国债的收益率看成无风险报酬率。风险报酬率高低与风险大小有关，风险越大，风险报酬率越大。）
风险价值的相关概念考点试题
大咖讲解：风险价值的相关概念
货币时间价值观念
（一）货币的时间价值概念
1、定义：也称资金的时间价值，指货币随着时间的推移而发生的增值。
货币的时间价值原理正确揭示了不同时点上的资金之间的换算关系，是财务决策的基础。
2、资金时间价值的两种表现形式
（1）相对数（时间价值率）：扣除风险报酬和通货膨胀因素后的平均资金利润率或平均报酬率。
（2）绝对数（时间价值额）：一定数额的资金与时间价值的率的乘积。
（一般情况下，可以用利率和利息代表时间价值）
（二）货币的时间价值计算
1、一次性收付款项的复利终值与现值
|
|
终值 |
现值 |
|
一次性收付款项 |
假设i为基期利率，n为计息周期数。P 为现值，F为终值，则复利终值的计算公式为： F= P（1+i）n=P（F/P，i，n） （1+i）n：复利终值系数，记为（F/P，i，n）。 |
P= F（1+i）-n= F(P/F，i，n) （1+i）-n：复利现值系数，记为（P/F，i，n） |
|
后付年金 |
假设每年的支付金额为 A，利率为i， 计息期数为 n，则计算公式为∶
年金终值系数，记为（F/A，i，n）。 |
年金现值系数，记为（P/A，i，n） |
|
先付年金 |
F=A[（F/A，i，n+1）-1] |
P=A[（P/A，i，n+1）-1] |
|
递延年金 |
/ |
P= A[(P/A，i，n)](1＋i)-m n：年金发生期数；m：递延期数 |
|
永续年金 |
/ |
P=A/i （一般优先股因为有固定的股利而无到期日，因此优先股有时可视为永续年金。） |
风险价值观念
（一）风险价值的相关概念
1、风险：指由于未来影响因素的不确定性而导致其财务成果的不确定性。
2、风险价值：又称风险收益、风险报酬，是指投资者由于冒着风险进行投资而获得的招过资金时间价值的额外收益。
风险报酬有两种表示方法∶风险报酬额和风险报酬率。
3、投资必要报酬率 =资金时间价值（无风险报酬率）＋ 风险报酬率
（一般情况下，可以将购买国债的收益率看成无风险报酬率。风险报酬率高低与风险大小有关，风险越大，风险报酬率越大。）
（二）单项资产（或单项投资项目）的风险衡量
|
风险衡量 |
内容 |
|
1、确定概率分布 |
将随机事件各种可能的结果按一定的规则进行排列，同时列出各种结果出现的相应概率，这一完整的描述称为概率分布。 （1）0≤Pi≤1；（2）所有结果的概率之和等于1。 |
|
2、计算期望报酬率 |
期望值：一个概率分布中的所有可能结果以各自相应的概率为权数计算的加权平均值。反映了预计报酬的平均化，即在不确定因素影响下，投资者的合理预期值。 期望报酬率： Ki：第i种可能结果的报酬率；Pi：第i种可能结果的概率；n：可能结果的个数 |
|
3、计算标准离差
|
标准离差：简称标准差，反映概率分布中各种可能结果对期望值的偏离或离散程度。 （标准离差是用绝对数来衡量决策方案的风险，在期望值相同的情况下，标准离差越小，说明离散程度小，风险也就越小。）
δ：期望报酬率的标准离差； Pi：第i种可能结果的概率；n：可能结果的个数 |
|
4、计算标准离差率 |
标准离差率：标准离差同期望报酬率的比值。 （在期望报酬率不同的情况下，标准离差率越大，风险越大；反之，标准离差率越小，风险越小。）
V：标准离差率；δ：标准离差； |
：期望报酬率；Ki：第i种可能结果的报酬率；
（三）风险报酬估计
风险报酬率=风险报酬系数×标准离差率×100%
即RR=b×V×100%
b：风险报酬系数（指将标准离差率转化为风险报酬率的系数。）
货币时间价值概念
1、定义：也称资金的时间价值，指货币随着时间的推移而发生的增值。
货币的时间价值原理正确揭示了不同时点上的资金之间的换算关系，是财务决策的基础。
2、资金时间价值的两种表现形式
（1）相对数（时间价值率）：扣除风险报酬和通货膨胀因素后的平均资金利润率或平均报酬率。
（2）绝对数（时间价值额）：一定数额的资金与时间价值的率的乘积。
（一般情况下，可以用利率和利息代表时间价值）
单项资产(或单项投资项目)的风险衡量
单项资产（或单项投资项目）的风险衡量
|
风险衡量 |
内容 |
|
1、确定概率分布 |
将随机事件各种可能的结果按一定的规则进行排列，同时列出各种结果出现的相应概率，这一完整的描述称为概率分布。 （1）0≤Pi≤1；（2）所有结果的概率之和等于1。 |
|
2、计算期望报酬率 |
期望值：一个概率分布中的所有可能结果以各自相应的概率为权数计算的加权平均值。反映了预计报酬的平均化，即在不确定因素影响下，投资者的合理预期值。 期望报酬率： Ki：第i种可能结果的报酬率；Pi：第i种可能结果的概率；n：可能结果的个数 |
|
3、计算标准离差
|
标准离差：简称标准差，反映概率分布中各种可能结果对期望值的偏离或离散程度。 （标准离差是用绝对数来衡量决策方案的风险，在期望值相同的情况下，标准离差越小，说明离散程度小，风险也就越小。）
δ：期望报酬率的标准离差； Pi：第i种可能结果的概率；n：可能结果的个数 |
|
4、计算标准离差率 |
标准离差率：标准离差同期望报酬率的比值。 （在期望报酬率不同的情况下，标准离差率越大，风险越大；反之，标准离差率越小，风险越小。）
V：标准离差率；δ：标准离差； |
风险报酬估计
风险报酬率=风险报酬系数×标准离差率×100%
即RR=b×V×100%
b：风险报酬系数（指将标准离差率转化为风险报酬率的系数。）
1.一次性收付款项的复利终值与现值
一次性收付款项的复利终值与现值
|
|
终值 |
现值 |
|
一次性收付款项 |
假设i为基期利率，n为计息周期数。P 为现值，F为终值，则复利终值的计算公式为： F= P（1+i）n=P（F/P，i，n） （1+i）n：复利终值系数，记为（F/P，i，n）。 |
P= F（1+i）-n= F(P/F，i，n) （1+i）-n：复利现值系数，记为（P/F，i，n） |
|
后付年金 |
假设每年的支付金额为 A，利率为i， 计息期数为 n，则计算公式为∶
年金终值系数，记为（F/A，i，n）。 |
年金现值系数，记为（P/A，i，n） |
|
先付年金 |
F=A[（F/A，i，n+1）-1] |
P=A[（P/A，i，n+1）-1] |
|
递延年金 |
/ |
P= A[(P/A，i，n)](1＋i)-m n：年金发生期数；m：递延期数 |
|
永续年金 |
/ |
P=A/i （一般优先股因为有固定的股利而无到期日，因此优先股有时可视为永续年金。） |
