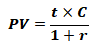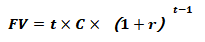考点1：年金的概念
年金（普通年金） | 一组在某个特定的时段内金额相等、方向相同、时间间隔相同、不间断的现金流。 |
永续年金 | 一组在无限期内金额相等、方向相同、时间间隔相同的现金流。 |
增长型年金 | 一组在某个特定的时段内方向相同、时间间隔相同、金额虽然不同但增长率相等的现金流。 |
增长型永续年金 | 在无限期内方向相同、时间间隔相同、金额虽然不同但增长率相等的现金流。 |
【2021真题】
1、下列关于年金的说法，正确的有（ ）
Ⅰ向租房者每月固定领取的租金可视为一种年金
Ⅱ定期定额缴纳的房屋贷款月供可视为一种年金
Ⅲ退休后从保险公司领取的养老金可视为一种年金
Ⅳ按月领取的奖励可视为一种年金
【李泽瑞老师计算题举例精讲：立即学习>>>】
考点2：年金的计算（★★）
年金终值和现值的计算通常采用复利的形式。
根据等值现金流发生的时间点的不同，年金可以分为：
1、期初年金：在一定时期内每期期初发生系列相等的收付款项，即现金流发生在当期期初，如生活费支出、教育费支出、房租支出等；
2、期末年金：现金流发生在当期期末，如房贷支出等。
年金现值 | 年金终值 | |
期末 | 年金的现值：为每年投资收益总和，它是一定时间内每期期末收付款项复利现值之和。 假设年金现值为PV，每年付款额为C，年利率为r，付款时间为t年，根据复利现值计算公式可得：
| 年金的终值：指一定时间内，每期期末收付的本利和，也就是将每一期的金额，按照复利计算到最后一期期末的终值的累加和。假设，年金终值为FV，每年付款额为C，年利率为r，付款时间为t年，根据复利现值计算公式可得：
|
期初 | 期初年金的现值等于期末年金现值的（1+r）倍，即：
| 期初年金终值等于期末年金终值的（1+r）倍，即：
|
3、永续年金、增长型永续年金
C：第一年现金流，r：利率，g：增长率
永续年金期末现值：PV=C/r
4、增长型年金
C：第一年现金流，r：利率，g：增长率
现值 | 终值 | |
PV=C×（1+r）-1+C×（1+g）×（1+r）-2+....+C×（1+g）t-1×（1+r）-t g：每年固定增长比率 | FV=C×（1+r）t-1+C×（1+g）×（1+r）t-2+C×（1+g）2×（1+r）t-2+...+C×（1+g）t-1 | |
当r≠g时 |
|
|
当r=g时 |
|
|
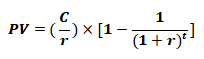
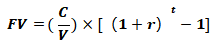
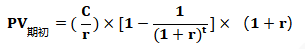
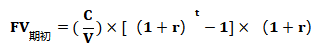
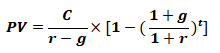
![9O~904WC04G1AEIF8SC0]JF.png](https://file.233.com/ess-files/ess-ecms-web/67BCA9CB163144B38B4F022A26B40DF5.png)
5、增长型永续年金
期末现值：PV=C/r-g
C：第一年现金流，r：利率，g：增长率
温馨提示：文章由作者233网校-py独立创作完成，未经著作权人同意禁止转载。
