第五节 风险管理的数理基础
一、收益的计量
(一)绝对收益绝对收益是对投资成果的直接衡量,反映投资行为得到的增值部分的绝对量。用数学公式表示为:
绝对收益=P—P。
其中,P为期末的资产价值总额,P。为期初投入的资金总额。
(二)百分比收益率
百分比收益率是当期资产总价值的变化及其现金收益占期初投资额的百分比。百分比收益率通常用百分数表示,是最常用的评价投资收益的方式。用数学公式表示为:
![]()

二、常用的概率统计知识
(一)预期收益率
由于投资风险的不确定性,资产或投资组合的未来收益往往也是不确定的。在风险管理实践中,为了对这种不确定的收益进行计量和评估,通常需要计算资产或投资组合未来的预期收益率(或期望收益率),以便于比较和决策。

(二)方差和标准差

方差的平方根称为标准差,用δ表示。在风险管理实践中,通常将标准差作为刻画风险的重要指标。资产收益率标准差越大,表明资产收益率的波动性越大。当标准差很小或接近于零时,资产的收益率基本稳定在预期收益水平,出现的不确定性程度逐渐减小。
(三)正态分布
正态分布是描述连续型随机变量的一种重要概率分布(见图l—1)。若随机变量2的概率密度函数为:
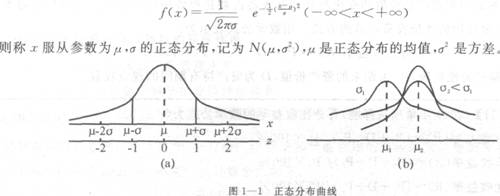


三、投资组合分散风险的原理

如果资产组合中各资产存在相关性,则风险分散的效果会随着各资产间的相关系数有所不同。假设其他条件不变,当各资产间的相关系数为正时,风险分散效果较差;当相关系数为负时,风险分散效果较好。。在风险管理实践中,商业银行可以利用资产组合分散风险的原理,将贷款分散到不同的行业、区域,通过积极实施风险分散策略,显著降低发生大额风险损失的可能性,从而达到管理和降低风险、保持收益稳定的目的。



































