两变量的散点图
进入经济师题库章节练习在线测试配套习题,可查看答案及解析 开始练习
两个变量问的关系可以用散点图来展示。在散点图中,每个点代表一个观测值,横纵坐标值分别代表两个变量相应的观测值。
图23—1是一些数据的散点图。横坐标值表示变量X的观测值,纵坐标值表示变量Y的观测值。图a的点几乎无规律而言,表示这两个变量不相关。图b和图e中,观测点密集在一条直线周围,表现为较强的线性相关,但相关的方向不同。图b中的两个变量为正相关关系,图c的两个变量为负相关关系。图d中的观测点呈现出曲线模式,这表示两个变量为非线性相关。(三)相关系数的定义和计算
相关系数是度量两个变量之间相关关系的统计量。常用的相关系数是Pearson相关系数,它度量的是两个变量之间的线性相关关系。
假设分别可得到两个变量X和Y的n组观测值,即xi,yi,i=1,2,…,n,其中的两组观测值之间是一一对应的.那么Pearson相关系数r的计算公式为:
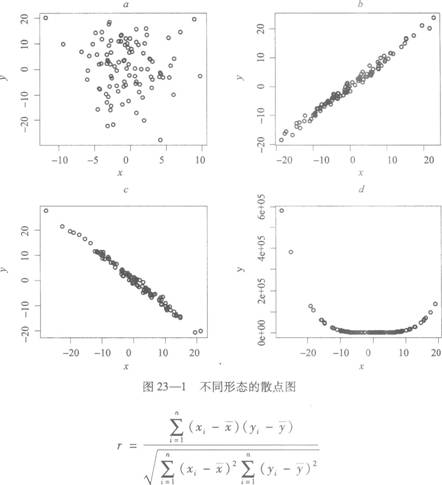
表23—1是1991年到2008年的城镇居民人均可支配收入和人均消费数据。图23—2是二者的散点图。从图中可看出,这两个变量呈正线性相关。



图23—1是一些数据的散点图。横坐标值表示变量X的观测值,纵坐标值表示变量Y的观测值。图a的点几乎无规律而言,表示这两个变量不相关。图b和图e中,观测点密集在一条直线周围,表现为较强的线性相关,但相关的方向不同。图b中的两个变量为正相关关系,图c的两个变量为负相关关系。图d中的观测点呈现出曲线模式,这表示两个变量为非线性相关。(三)相关系数的定义和计算
相关系数是度量两个变量之间相关关系的统计量。常用的相关系数是Pearson相关系数,它度量的是两个变量之间的线性相关关系。
假设分别可得到两个变量X和Y的n组观测值,即xi,yi,i=1,2,…,n,其中的两组观测值之间是一一对应的.那么Pearson相关系数r的计算公式为:

表23—1是1991年到2008年的城镇居民人均可支配收入和人均消费数据。图23—2是二者的散点图。从图中可看出,这两个变量呈正线性相关。



进入经济师题库章节练习在线测试配套习题,可查看答案及解析 开始练习
| �γ�רҵ���� | ��ʦ | ԭ��/�Żݼ� | ������� | ���� |
|---|---|---|---|---|
| ��������רҵ֪ʶ��ʵ��߶˰ࣨ�������û��������ͽ̲ģ� | ������ | ��3860 / ��1980 |  |
|
| �������̹���רҵ֪ʶ��ʵ��߶˰ࣨ�������û��������ͽ̲ģ� | ��� | ��3860 / ��1980 |  |
|
| ����������Դרҵ֪ʶ��ʵ��߶˰ࣨ�������û��������ͽ̲ģ� | ���� | ��3860 / ��1980 |  |
|
| ��������˰��רҵ֪ʶ��ʵ��߶˰ࣨ�������û��������ͽ̲ģ� | ���� | ��3860 / ��1980 |  |
|
| �м�����רҵ֪ʶ��ʵ��߶˰ࣨ�������û��������ͽ̲ģ� | ������ | ��3860 / ��1980 |  |
|
| �м����̹���רҵ֪ʶ��ʵ��߶˰ࣨ�������û��������ͽ̲ģ� | ���� | ��3860 / ��1980 |  |





