16、根据以下案例,回答后面的问题。
教学过程:
习旧引新
(1)在⊙O上,任取三个点A、B、C,然后顺次连接,得到的是什么图形?这个图形与⊙O有什么关系?
(2)由圆内接三角形的概念,能否得出什么是圆的内接四边形呢(类比)?
概念学习
(1)什么叫圆的内接四边形?
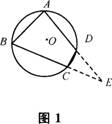
(2)如图1,说明四边形ABCD与⊙O的关系。
探讨性质
(1)前面我们已经学习了一类特殊四边形——平行四边形,矩形,菱形,正方形,等腰梯形的性质,那么要探讨圆内接四边形的性质,一般要从哪几个方面入手?
(2)打开《几何画板》,让学生动手任意画⊙O和⊙O的内接四边形ABCD。(教师适当指导)
(3)量出所有值(圆的半径和四边形的边,内角,对角线,周长,面积),并观察这些量之间的关系。
(4)改变圆的半径大小,这些量有无变化?由(3)观察得出的某些关系有无变化?
(5)移动四边形的一个顶点,这些量有无变化?由(3)观察得出的某些关系有无变化?移动四边形的四个顶点呢?移动三个顶点呢?
(6)如何用命题的形式表述刚才的实验得出来的结论呢?(让学生回答)
性质的证明及巩固练习
(1)证明猜想
(2)完善性质
①若将线段BC延长到E,那么,∠DCE与∠BAD又有什么关系呢?
②圆的内接四边形的性质定理:圆内接四边形的对角互补,并且任何一个外角都等于它的内对角。
(3)练习。
例题讲解
小结:为了使学生对所学的内容有一个完整而深刻的印象,让学生组成小组,从概念,性质,方法,特殊性进行讨论,然后对讨论的结果进行归纳。
(1)本节课我们学习了圆内接四边形的概念及圆内接四边形的主要性质,要求同学们理解圆
内接四边形和四边形的外接圆的概念,理解圆内接四边形的性质定理,并初步应用性质定理进行有关命题的证明和计算。
(2)我们结合《几何画板》的使用导出了圆内接四边形的性质,在这一过程中用到了许多数学方法(实验,观察,类比,分析,归纳,猜想等),同学们要逐步学会并应用这些方法去探讨有关的数学问题,提高我们的数学实践能力与创新能力。
问题:(1)一般数学概念的学习包括哪几个方面的内容?
(2)概念的获取一般有哪些形式?
(3)谈谈你对该案例的看法。专题推荐:2014年各学科教学能力试题 深入考点
真题推荐:2014上半年学科知识与教学能力真题 233网校真题解析班,全面分析考卷!

