1.B
【解析】持有期年均收益率
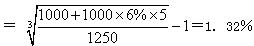
2.A
【解析】对于持有期限长于1年的债券投资而言,持有期年均收益率指的是按照复利折现计算的使持有期间的现金流入现值等于购买价格的折现率,假设所求的持有期年均收益率为r,则有:1250=1000×(F/P,6%,5)×(P/F,r,3),解得:r=2.30%或=
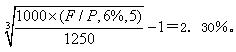
3.B
【解析】未来三年净现金流量的现值=10000×(P/F,6%,1)+15000X(P/F,6%,2)+20000×(P/F,6%,3)=39576(万元),所以本题答案为B。
4.C
【解析】债券的发行价格=发行时的债券价值=1000×5%×(P/A,6%,10)+1000×(P/F,6%,10)=50×7.3601+1000×0.5584=926.41(元)
5.A
【解析】本题是典型的计算即付年金现值的问题,1000×(P/A,10%,6)×(1+10%)=4790.83(元)。
6.B
【解析】即付年金终值=普通年金的终值×(1+i),在年金、期限和利率相同的前提下,即付年金终值大于普通年金的终值。
7.B
【解析】本题是计算永续年金现值问题,答案为:40000/5%=800000(元)。
8.D
【解析】10×(F/P,2%/2,5×2)=10×(F/P,1%,10)=11.046(万元)
9.C
【解析】本题是单利现值的计算问题:39200/(1+4%×3):35000(元)。
10.B
【解析】普通年金现值=一定时期内每期期末等额收付款项的复利现值之和,故五年期的普通年金现值系数=O.9091+0.8264+0.7513+O.6830+0.6209=3.7907。
11.B
【解析】普通年金终值系数(F/A,i,n)=[(F/P,i,n)一1]/i,偿债基金系数(A/F,i,n)=i/[(F/P,i,n)一1],所以普通年金终值系数与偿债基金系数互为倒数,即B错误。
12.D
【解析】建立的偿债基金=40000/(F/A,3%,5)=7534(元)
13.B
【解析】利率为10%,4年期的先付年金现值系数=(P/A,10%,4)×(1+lO%)=(O.9091+ O.8264+0.7513+O.6830)×(1+10%)=3.4868
14.A
【解析】即付年金终值系数是在普通年金终值系数基础之上,期数加1,系数值减1,即10年10%的即付年金终值系数=(F/A,10%,11)一1=18.531—1=17.531。
15.B
【解析】根据题目条件可知半年的收益率一20/1000=2%,所以年名义收益率=2%×2=4%,年实际收益=(1+2%)2一1=4.04%,年实际收益率一年名义收益率=0.04%。
16.C
【解析】根据题意可知债券的到期日是2006年1月1日,投资者持有该债券的期限为0.25年,所以短期持有债券的持有期收益率=[1000×10%+(1000—1020)]/1020×100%=7.843%,持有期年均收益率=7.843%/0.25=31.37%。
17.C
【解析】长期持有、股利稳定不变的股票的内在价值一每年固定的股利/投资人要求的必要报酬率,本题中股票的内在价值=6/7%=85.71(元),股票的内在价值是投资者能够接受的购买价格的上限,如果买价高于内在价值,投资者不会购买。
18.D
【解析】根据资本资产定价模型可知该股票的必要收益率=10%+1.3×(16%一10%)=17.8%,根据股利固定增长的股票估价模型可知,该股票的内在价值=8×(1+6%)/(17.8%一6%)=71.86(元)。
19。C
【解析】股票的购买价格=股利和售价按照持有期年均收益率折现的现值之和,515=50×(P/F,i,1)+60×(P/F,i,2)+(80+600)×(P/F,i,3)通过测试可知,当折现率为18%时,购买价格为499.32元;当折现率为16%时,购买价格为
523.37元;利用内插法可知,该题答案为16%+(523.37—515)/(523.37—499.32)×(18%一16%)=16.70%。
20.C

21.B
【解析】由于剩余年限(3个月)在一年以内,因此应该按照债券持有期间的收益额除以买入价计算持有期收益率。由于本题中的到期本息和=1000×(F/P,4%,5)=1000×1.2167=1216.7(元),债券买入价为1100元,因此,持有期收益率=(1216.7—1100)/1100×100%=10.61%,持有期年均收益率=10.61%/(3/12)=42.44%。
22.C
【解析】持有期收益率=(10.5—10+1.5)/10×100%=20%,持有期年均收益率=20%/(3/12)=80%。
23.A
【解析】根据“每半年末等额偿还”可知本题属于普通年金问题,进一步分析可知,本题属于已知普通年金现值、折现率和折现期数,计算普通年金(A),即属于计算年资本回收额问题。所以,答案为:A=50000/(P/A,2%,10)=5566(元)。
24.A
【解析】在名义利率相同的情况下,1年内复利计息次数越多,实际利率越高。注意:本题是针对“债券发行企业”而言的,债券发行企业属于筹资方,要支付利息,因此,实际利率越低对其越有利。所以,该题答案应该是A。
二、多项选择题
1.BD
【解析】根据“前3年无流入,后5年每年年初流入1000元”可知,第一次现金流入发生在第4年初,所以,属于递延年金,不属于即付年金。确定递延期时一定注意应将期初问题转化为期末,本题中第一次现金流入发生在第4年初相当于第3年末,因此,递延期m=3—1=2。
2.ABC
【解析】(1)普通年金的终值是指把每期等额的数值换算为最后一期期末的数值再求和。5期的年金终值,可以考虑先把最后的四期换算成最后一期的数值再求和,其普通年金终值系数为(F/A,10%,4),再把第一期期末的数值折算成第5期期末的数值,应往后推4期,其复利终值系数为(F/P,10%,4),两个系数相加就是5期的年金终值系数,所以A选项正确,D选项错误。
(2)普通年金的现值是指把每期等额的数值换算为第一期期初的数值再求和。5期的年金,可以考虑先将最初的四期数值贴现求和,其年金现值系数为(P/A,10%,4),再将第5期期末的数值单独贴现,其复利的现值系数为(P/F,10%,5),两个系数相加就是5期的年金现值系数,所以B选项正确。
(3)把4期的普通年金的现值A×(P/A,10%,4)换算为普通年金的终值,只要往后推4期,即乘4期的复利终值系数(F/P,10%,4),而4期普通年金的终值为AX(F/A,10%,4),所以C选项正确。本题还可以这样理解:
(1)根据:
(F/A,i,n)=1+(1+i)1+…+(1+i)n-1
可知:(F/A,10%,5)=1+(1+10%)1+(1+10%)2+(1+10%)3+(1+10%)4
(F/A,10%,4)=1+(1+10%)1+(1+10%)2+(1+10%)3
所以,(F/A,10%,5)=(F/A,10%,4)+(1+lO%)4=(F/A,10%,4)+(F/P,10%,4)即A选项正确,而D选项错误。
(2)根据:(P/A,i,n)=(1+i)-1+(1+10%)-2+…+(1十lO%)-n
可知:(P/A,10%,5)=(1+10%)-1+(1+10%)-2+(1+10%)-3+(1+10%)-4+(1+
10%)-5
(P/A,10%,4)=(1+10%)-1+(1+10%)-2+(1+10%)-3+(1+10%)-4
即,(P/A,10%,5)=(P/A,10%,4)+(1+10%)-5
所以,(P/A,10%,5)=(P/A,10%,4)+(P/F,10%,5),因此,B选项正确。
(3)根据:(F/P,i,n)=(1+i)n
可知:(F/P,10%,5)=(1+10%)5
根据:(P/A,i,n)=[1一(1+i)-n]/i
可知:(P/A,10%,5)=[1一(1+10%)-5]/10%
根据:(F/A,i,,n)=[(I-Fi)n-1]/i
可知:(F/A,10%,5)=[(1+10%)5一1]/10%
所以,(F/P,10%,5)×(P/A,10%,5)=(F/A,10%,5),因此,C选项正确。
3.ABCD
【解析】(P/F,12%,5)=1/(F/P,12%,5)=0.5674,(F/A,12%,5)=[(F/P,12%,5)一1]/12%=6.3525,(P/A,12%,5)一[1一(P/F,12%,5)]/12%=3.6050,(A/P,12%,5)=1/(P/A,12%,5)=O.2774。
4.BC
【解析】13000=5000×(P/A,i,3),所以,(P/A,i,3)=13000/5000=2.60,查表可知,(P/A,7%,3)=2.6243,(P/A,8%,3)=2.5771,因此可知该题的借款利率大于7%小于8%。
5.ABC
【解析】假设能足额取款的时间是第n年末,则n应该满足的条件是1000×(P/A,5%,n)小于或等于10000,即(P/A,5%,n)小于或等于10。查阅年金现值系数表可知,本题答案选择ABC。
6.AB
【解析】长期持有、股利固定增长的股票内在价值V=D0×(1+g)/(K—g)=D1/(K—g),可以看出,股票的内在价值与预期第一年的股利(D1)同方向变化;因为股利年增长率g越大,计算公式中的分母越小,分子越大,股票内在价值越大,所以股票的内在价值与股利年增长率同方向变化。
7.AB
【解析】票面收益率又称名义收益率或息票率,是印制在债券票面上的固定利率,通常是年利息收入与债券面额的比率,所以A不正确;本期收益率=债券年利息/1责券买入价×100%,不能反映债券的资本损益情况。
8.ABD
【解析】衡量债券收益水平的尺度为债券收益率。决定债券收益率的因素主要有债券票面利率、期限、面值、持有时间、购买价格和出售价格。
9.ABCD
【解析】一般而言,债券的基本要素包括:债券的面值、债券的期限、债券的利率和债券的价格。
10.ABCD
【解析】股价指数是指金融机构通过对股票市场上一些有代表性的公司发行的股票价格进行平均计算和报考对比后得出的数值。股价指数的计算方法有简单算术平均法、综合平均法、几何平均法和加权综合法等。
11.AB
【解析】利随本清的债券即到期一次还本付息债券。市场利率=6%+2%=8%,发行时债券的价值=(1000+1000×10%×5)×(P/F,8%,5)=1020.9(元),如果债券价格低于债券价值,则适合购买,所以,该题答案为AB。
12.ACD
【解析】资金时间价值相当于没有风险和通货膨胀情况下的利率,因此,纯利率就是资金时间价值,所以A选项正确;由于社会平均资金利润率包含风险和通货膨胀因素,所以B选项错误;由于国库券几乎没有风险,所以,通货膨胀率极低时,可以用国债的利率表示资金时间价值,因此,C选项正确;无风险收益率是资金时间价值和通货
膨胀补偿率之和,不考虑通货膨胀下的无风险收益率就是资金时间价值,所以,D选项正确。
13.BCD
【解析】本期收益率=直接收益率=债券年利息收入/1责券买入价×100%;息票率=票面收益率=债券年利息收入/1责券面值×100%;短期的持有期收益率=[债券持有期间的利息收入/债券买入价+(卖出价一买入价)/1责券买入价]×100%=债券持有期间的利息收入/1责券买入价×100%+资本利得收益率。
14.BCD
【解析】普通股评价模型的局限性:(1)未来经济利益流入量的现值只是决定股票价值的基本因素而不是全部因素;(2)模型对未来期间股利流入量预测数的依赖性很强,而这些数据很难准确预测。股利固定不变、股利固定增长等假设与现实情况可能存在一定差距;(3)股利固定模型、股利固定增长模型的计算结果受D0或D1的影响很大,而这两个数据可能具有人为性、短期性和偶然性,模型放大了这些不可靠因素的影响力;(4)折现率的选择有较大的主观随意性。
15.AC
【解析】计息期利率=r/m,共计计息m×n次,所以,复利终值F=PX(1+r/m)mn,即C选项正确;又因为[F/P,(1+r/m)m-1,n]一[1+(1+r/m)m-1]n一(1+r/m)nm,所以,A选项也正确。
16.ABCD
【解析】递延年金现值=AX(P/A,i,n)×(P/F,i,m)或A×[(P/A,i,m+n)一(P/A,i,m)]或A×(F/A,i,n)×(P/F,i,n+m),其中,m为递延期数,n为等额收付的次数。该题的年金是从第七年年初开始,即第六年年末开始,所以,递延期为5期,即m=5;由于共计支付10次,因此,n=10。因此,ABD选项正确。另外,根据年金现值系数和复利现值系数的表达式可知,(P/A,i,n)=[1一(P/F,i,n)]/i,因此,C选项也正确。
17.BCD
【解析】本题是即付年金求终值的问题,即付年金终值系数有两种计算方法:一是普通年金终值系数×(1+i),由此可知,B、C选项正确;一种是在普通年金终值系数的基础上期数+l,系数一1,由此可知,D选项正确。
18.BCD
【解析】年金指的是系列等额收付的款项,零存整取储蓄存款的“整取额”属于一次性收付款项,不属于年金;定期定额支付的养老金、年资本回收额(E知现值求出的年金)、偿债基金(E知终值求出的年金)则都属于普通年金形式。
三、判断题
】.×
【解析】递延年金有终值,但是终值的大小与递延期无关,递延年金的终值=年金×(F/A,i,,n),其中n表示等额收付的次数(年金A的个数),显然其大小与递延期m无关。
2.×
【解析】股利固定增长模型的使用条件包括两个:(1)股利增长率固定不变;(2)长期持有股票(即不 准备出售股票)。
3.×
【解析】对股票投资的未来现金流入进行折现时,如果折现率是预期报酬率,则现值等于股票市价;如果折现率是投资者要求的必要报酬率,则现值等于股票价值。由于计算现值时,折现率在分母上,因此,折现率越高,现值越小。所以,正确的说法应该是:如果股票市价低于股票价值,则股票投资的预期报酬率高于投资者要求的必要报酬率。
4.√
【解析】根据普通年金现值系数(P/A,i,n)的数学表达式、复利终值系数(F/P,i,n)的数学表达式以及复利现值系数(P/F,i,n)的数学表达式,可知,(P/A,i,n)=[1—1/(F/P,i,n)]/i,所以,(P/A,5%,5)=(1—1/1.2763)/5%=4.3297,(A/P,5%,5)=1/(P/A,5%,5)=1/4.3297=0.231。
5.×
【解析】设每年年初存入的资金的数额为A元,则:第一次存入的资金在第三年末的终值为A×(1+4%×3)=1.12A第二次存入的资金在第三年末的终值为A×(1+4%×2)=1.08A
第三次存入的资金在第三年末的终值为AX(1+4%)=1.04A所以,第三年末的资金总额=1.12A+1.08A+1.04A=3.24A即,3.24A=32400,所以,A=10000注意:因为是单利计息,所以,该题不是已知终值求年金的问题,不能按照即付年金终值公式计算。
6.√
【解析】首先应该注意每半年计息一次时“年利率”指的是“名义利率”不是“实际利率”,即:1000×(F/P,i/2,8)=2000,(F/P,i/2,8)=2,查表可知:(F/P,10%,8)=2.1436,(F/P,9%,8)=1.9926,利用内插法可知:(2.1436—2)/(2.1436一1.9926)=(10%一i/2)/(10%一9%),解得:i/2=9.05%,i=18.10%,
7.√
【解析】如果给定的是一个以即付年金形式表示的永续年金,则其现值为:P—A+A/i。这是因为永续年金的现值公式是在假定永续年金是普通年金形式的基础上推出来的,如果是即付年金的形式,可以把第一期期初的等额收付A单独考虑,即:P=A+A/i=20+20/10%=220(万元)。
8.×
【解析】即付年金是指从第一期起,在一定时期内每期期初等额收付的系列款项,又称先付年金。它与普通年金的区别仅在于付款时间的不同。即付年金的终值是其最后一期期末时的本利和,是各期收付款项的复利终值之和。即付年金终值(F)=年金(A)×即付年金终值系数,“即付年金终值系数”可以用[(F/A,i,n+1)一1]表示,即在普通年金终值系数的基础上,期数加1,系数减1所得的结果。
9.√
【解析】年金是指系列等额的收付行为,其间隔期间只需要满足“相等”的条件即可,间隔期间完全可以不是1年,例如:每半年支付一次利息的债券利息构成的也是年金。
10.×
【解析】债券的收益主要包括两方面的内容:一是债券的利息收入;二是资本损益(债券买入价与卖出价之间的差额)。
11.×
【解析】股票的收益由股利和资本利得两方面组成,主要取决于股份公司的经营业绩和股票市场的价格变化,但与投资者的经验和技巧也有一定的关系。
12.×
【解析】股票价格有广义和狭义之分,狭义的股票价格就是股票交易价格。广义的股票价格则包括股票的发行价格和交易价格两种形式。股票交易价格具有事先的不确定性和市场性特点。
13.√
【解析】(1)利率升高时,投资者会选择安全又有较高收益的储蓄,从而大量资金从证券市场中转移出来,造成证券供大于求,股价下跌;反之,股价上涨;(2)利率上升时,企业资金成本增加,利润减少,从而企业派发的股利将减少甚至发不出股利,引起股价下跌;反之,引起股价上涨。
四、计算题
1.【答案】
比较三种付款方案支付款项的现值,选择现值最小的方案。
方案(1)P=20×(P/A,10%,10)×(1+10%)=135.18(万元)
方案(2)P=25×(P/A,10%,10)×(P/F,10%,4)=104.92(万元)
方案(3)P=24×(P/A,10%。10)×(P/F,10%,3)=ll0.79(万元)
该公司应该选择第二个方案。
2.【答案】
由于每次的还款额相等,所以,属于年金。由于100万元是现在的价值(即现值),所以,属于已知年金现值求年金问题,即A×(P/A,i,n)=1000000,本题中共计还款20×12=240(次),因此,n=240,由于月利率为6%/12=O.5%,所以,i=0.5%,即:A=1000000/(P/A,0.5%,240)=1000000/139.5808=71 64(元)。
3.【答案】
该题可以采用三种常见的方法解答:方法一:由于下一年初就是上一年末,所以,本
题完全可以理解为从2001年开始,每年年末存入10000元.计算2004年末的本利和,因此.是标准的期数为4的普通年金终值计算问题。
F=10000×(F肌,10%,4)
=10000×4.64lO
=464 10(元)
另外完全可以按照先付年金计算.可以有两种方法:
方法二:先按照即付年金计算前三次存款的终值10000×(F/A,10%,3)×(1+10%)
注意:10000×(F/A,10%,3)×(1+10%)表示的是2004年末的数值然后,加上最后一次存款,即:10000×(F/A,10%,3)×(1+10%)+10000=46410(元)。
方法三:先按照即付年金计算四次存款的终值10000×(F/A,10%,4)×(1+10%),由于表示的是2005年末的数值.所以。应该复利折现一期。折算到2005年初;
即,10000×(F/A,10%.4)×(1+10%)×(17/F,10%,1)
=10000×(F/A,10%,4)
=46410(元)
4.【答案】
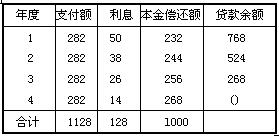
表中数字计算过程:
年支付额(A)=P÷(P/A,5%,4)
=1000÷3.5460=282(万元)
第一年支付额=282(万元)
利息=贷款余额×5%一1000×5%=50(万元)
本金偿还额=支付额一利息
=282—50=232(万元)
贷款余额=上期贷款余额一本期本金偿还额
=1000一232=768(万元)
第二年、第三年类推。
5.【答案】提示:
(1)假定公司没有增发普通股计划(即普通股股数不变),所以,股利增长率一每股股利增长率。本题中“第四年及以后”的每股股利增长率=O,均等于第三年的每股股利;
(2)对各期的股利逐个贴现求和得出的就是股票的价值。不过注意:虽然前两年的股利增长率均为10%,数值相等,但是不能按照“股利固定增长模型”计算其现值,因为股利固定增长模型适用于“长期”固定增长的情况(即如果在有限的年度内固定增长,不能按照这个模型计算).因此。第年、第二年每股股利需要单独贴现;
(3)第三年及以后各年每股股利相同,并且没有确定的期限,因此。可以套用股利固定模型的计算公式,但注意直接计算得出的是第二年年未的数值,所以还要再乘以(P/F,12%。2).折算到第一在年初。
该题答案如下:
预计第1年的每股股利=2×(1+10%)=2.2(元)
预计第2年的每股股利
=2.2×(1+1O%)=2.42(元)
预计第3年及以后备年的每股股利
=2.42×(1+8%)=2.614(元)
股票的价值
=2.2×(P/F,12%,1)+2.42×(P/F,12%,
2)+(2.614/12%)×(P/F,12%,2)
=1.964+1.929+17.366=21.26(元)
6.【答案】
本题的债券属于分期付息、到期一次还本债券,其内在价值计算公式为:
P=1000×6%×(P/A,8%,6)+1000×(P/F,
8%,6)
=60×4.6229+1000×O.6302
=907.57(元)
即这种债券的价格必须低于907.57元时,该企业才会购买。
7.【答案】
(1)x公司股票的股利预计每年均以6%的增长率增长,上年每股股利为O.10元,投资者要求的必要报酬率为8%,代入股利固定增长模型可知:
P(X)=O.10×(1+6%)/(8%一6%)
=5.3(元/股)
Y公司每年股利稳定不变,每股股利O.5元,代入股利固定模型可知:
P(Y)=O.50/8%=6.25(元/股)
(2)由于x公司股票现行市价8元高于其投资价值5.3元,故x公司股票目前不宜投资购买。Y公司股票现行市价为6元低于其投资价值6.25元,故Y公司股票值得投资,ABC企业应购买Y公司股票。
8.【答案】
(1)本期收益率=(1000×8%/1020)×100%
=7.84%
(2)持有期收益率=(1060—1020)/1020×100%
=3.92%
持有期年均收益率=3.92%/0.5=7.84%
(3)持有期收益率
=[1000×8%+(1000—1020)]/1020×100%
=5.88%
持有期年均收益率=5.88%/(10/12)=7.06%
(4)1020
=1000×8%×(P/A,i,2)+1000X(P/F,i,2)
经过测试得知:
当i=7%时,1000×8%×(P/A,7%,2)+1000×(P/F,7%,2)=1018.04
当i=6%时,1000×8%×(P/A,6%,2)+1000×(P/F,6%,2)=1036.67
用内插法计算可知:
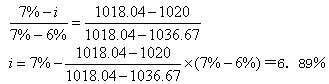
即持有期年均收益率为6.89%。
9.【答案】
(1)本期收益率=1.5/8.5×100%=17.65%
(2)持有期收益率=(10.5—10)/10X 100%=5%
(3)10=1×(P/a,i,2)+11×(P/F,i,2)
经过测试得知:
当i=14%时,
1×(P/A,i,2)+11×(P/F,i,2)
=10.1112
当i=16%时,
1×(P/A,i,2)+11×(P/F,i,2)
=9.7804
用内插可知:
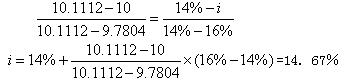
即:持有期年均收益率为14.67%
10.【答案】
(1)计算以下指标:
①甲公司证券组合的β系数
=50%×2+30%×1+20%×O.5=1.4
②甲公司证券组合的风险收益率
=1.4×(15%一10%)=7%
③甲公司证券组合的必要投资收益率
=10%+7%=17%
④投资A股票的必要投资收益率
=10%+2×(15%一10%)=20%
(2)因为,A股票的内在价值=1.2×(1+8%)/
(20%一8%)=10.8(元)小于当前的股价12元
(或:A股票的预期收益率R=D1/P+g=1.2×
(1+8%)/12+8%=18.8%小于必要投资收益率
20%),所以,甲公司当前出售A股票比较有利。
11.【答案】
第1年的每股股利为l×(1+4%)=1.04(元)
第2年的每年股利=1.04×(1+5%)=1.092(元)
第3年的每股股利=1.092X(1+5%)=1.147(元)
第4年的每股股利=1.147X(1+5%)=1.204(元)
第5年的每股股利=1.204X(1+5%)=1.264(元)
股票价值
=1.04×(P/F,10%,1)+1.092×(P/F,10%,
2)+1.147×(P/F,10%,3)+1.204×(P/F,
10%,4)+(1.264+25)×(P/F,10%,5)
=O.9455+O.9024+O.8617+O.8223+16.3073
=19.84(元)
由于低于股票市价22元,因此,不值得购买。


