一、数额法
数额法(绝对量值法)—是对资金时间价值的具体应用,将现金流量换算成净现值(NPV)、净年值(AW)、净将来值(PW),按照上述值大于、小于或等于零来判断方案是否接受。
应用分析
某方案现时点投资23万元,此后从第2年年末开始,连续20年,每年将有6.5万元的净收益,净残值为6.5万元。若基准收益率为20%,己知:(P/A,20%,20)=4.8696,(P/F,20%,21)=0.0217,则该方案的净现值是()万元。
A. 2.57
B. 3.23
C. 3.52
D. 4.35
答案:C
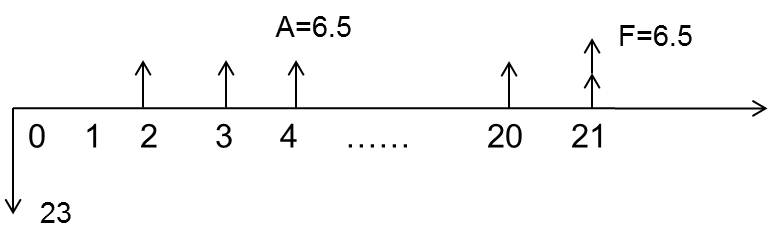
【解析】
先画现金流量图。
把每年净收益A=6.5万,折为第2年初第1年末现值(此处为A→P的转换,每年的净收益6.5万元是年值A,是从第2年年末开始的,折现后,P值在第一个A值的前一时间点1上,即:第1年年末,第2年年初)
P1=A(P/A,20%,20)=6.5×4.8696=31.6524
把时间点1上的净收益继续折为0点位置上的现值(此时为F→P的转换):
P2=P1/(1+r)=31.6524/120%=26.377
把净残值折为现值(F→P):
P3=F(P/F,20%,21)=6.5×0.0217=0.14105
所以,净现值=26.377+0.14105-23=3.52
即:PW=6.5(P/A,20%,20)(P/F,20%,1)+6.5(P/F,20%,21)-23=3.52
易错处:
①将20年收益折现时,忘记只折在第1年年末,还需要再折算一次,折到0点位置。
②忘记残值也需要折现。
③忘记最后减去初始投资23万元。
比率法(相对数法) 被广泛采用的是内部收益率法。
(1)内部收益率(IRR)的概念 使投资方案各年现金流量的净现值(净将来值、净年值)等于零时的利率。即:各年现金流入量的总现值(将来值、年值)与各年现金流出量的总现值(将来值、年值)相等的折现率(PW=0或FW=0、AW=0时的折现率)

































