六、教学设计题(本大题1小题,30分)
17.下面是人教版义务教育数学教科书七年级上册的内容,据此回答下列问题。
1.2.4绝对值
两辆汽车从同一处0出发,分别向东、西方向行驶10 km,到达A,B两处(图1.2-6)。
它们的行驶路线相同吗?它们的行驶路程相等吗?
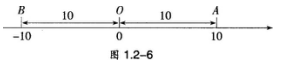
一般地,数轴上表示数a的点与原点的距离叫作数a的绝对值(absolute value),记作|a|。例如,图1.2—6中A,B两点分别表示10和-10,它们与原点的距离都是10个单位长度.所以10和-10的绝对值都是10.即
|10|=10,|-10 |=10。
显然|0|=0。
由绝对值的定义可知:这里的数a可以是正数、负数和0.
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。即
(1)如果a>0,那么|a|=a;
(2)如果a=0,那么|a|=a;
(3)如果a<0,那么|a|=-a。
练习:
1.写出下列各数的绝对值:
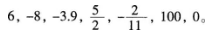
2.判断下列说法是否正确:
(1)符号相反的数互为相反数:
(2)一个数的绝对值越大,表示它的点在数轴上越靠右:
(3)一个数的绝对值越大,表示它的点在数轴上离原点越远:
(4)当a≠0时,|a|总是大于0。
3.判断下列各式是否正确:
(1)|5|=|-5|;(2)-|5|=|-5|;(3)-5=|-5|。
问题:
(1)学生学习绝对值这一节内容的知识背景:
(2)写出这节课的教学重难点;
(3)设计教学过程。
(1)学生在学习了有理数、数轴、相反数等概念后,能够用数轴上的点表示有理数,知道数轴上的点到原点的距离,并能比较这些距离的大小,已经具备了一定的数形结合的能力。
(2)教学重点:①初步理解绝对值的意义;②会求一个有理数的绝对值。
教学难点:①有理数绝对值概念的形成及运用;②用数形结合的思想理解绝对值的意义。
(3)教学过程:
一、创设情境,导入新课
出示PPT让学生观察图片中有两只小狗、一头大象分别距原点多远。设置问题:
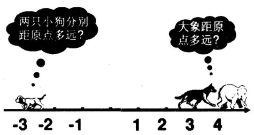
问题1:右边这只小狗距原点有多远?左边这只小狗距原点有多远?两只小狗距原点的距离相同吗?
问题2:两只小狗在数轴上对于的数分别是什么?
问题3:大象距原点的距离有多远?它比右边这只小狗距原点远还是近?
设计意图:利用动画展示,学生在有趣的问题情境中获取对绝对值概念的感性认识.并激发学生学习的积极性与主动性。
二、学习新课,理解概念
1.引入绝对值的概念
一般地,数轴上表示数a的点与原点的距离叫作数a的绝对值。记作|a|。
2.理解绝对值的概念
由刚才的图片知道两只小狗所在的位置到原点的距离都是3,也就是说3和-3的绝对值都是3:大象距原点的距离是4,那么4的绝对值就是4。即|3|=3,|-3|=3,|4|=4。
3.给出几对相反数,在课堂上讨论它们的绝对值,然后引发学生思考,互为相反数的数的绝对值有什么关系?
结论:互为相反数的两个数的绝对值相等。
4.让学生两两之间为一组,每人分别写三个正数、三个负数和零.让对方写出这些数的绝对值。观察有什么发现,引导学生总结绝对值的性质。
结论:正数的绝对值是它本身:负数的绝对值是它的相反数;0的绝对值是0。
三、知识巩固
学生自己完成练习1。
大家一起讨论,并提问,完成练习2,3。
四、课堂小结
教师资格考试数学学科知识与教学能力(初级中学)
微信扫码下面二维码进入教师资格微信学习群。

备考推荐:历年教师资格证真题及答案
热点推荐:教师资格证试题库
零基础如何备考?233网校零基础取证班购课即送教材,5大基础班级教学,给您备考指路,免费试听>>



