三、解答题(本大题1题, 10分)
14.设R2为二维欧式平面，F是R2到R2的映射，如果存在一个实数
，
，使得对于任意的P，Q∈R2，有d（F（P），F（Q））≤
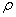d（P，Q），（其中d（P，Q）表示P，Q两点间的距离），则称F是压缩映射。
设映射T：R2→R2，
（1）证明：映射T是压缩映射；（4分）
（2）设P0=P0（x0，y0）为R2中任意一点，令Pn=T（Pn-1），n=1,2,3，…，证明：n→∞时，平面点列{Pn}收敛，并求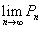
。（6分）
参考解析：
| 免费注册233网校会员，获取教师资格证真题！点击注册>> |
面试报考：2019上半年教师资格证面试报名时间
