根据人们对风险的偏好将其分为风险回避者、风险追求者和风险中立者。
1.风险回避者
风险回避者选择资产的态度是：当预期收益率相同时，偏好于具有低风险的资产；而对于具有同样风险的资产，则钟情于具有高预期收益率的资产。
2.风险追求者
与风险回避者恰恰相反，风险追求者通常主动追求风险，喜欢收益的动荡胜于喜欢收益的稳定。他们选择资产的原则是：当预期收益相同时，选择风险大的，因为这会给他们带来更大的效用。
3.风险中立者
风险中立者通常既不回避风险，也不主动追求风险。他们选择资产的惟一标准是预期收益的大小，而不管风险状况如何。
第二节 资产组合的风险与收益分析
一、资产组合的风险与收益
（一）资产组合
两个或两个以上资产所构成的集合，称为资产组合。如果资产组合中的资产均为有价证券，则该资产组合也可称为证券组合。
（二）资产组合的预期收益率[E（RP）]
资产组合的预期收益率，就是组成资产组合的各种资产的预期收益率的加权平均数，其权数等于各种资产在整个组合中所占的价值比例。即：
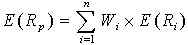式中，E（Ri）表示第i项资产的预期收益率；Wi表示第i项资产在整个组合中所占的价值比例。
（三）资产组合风险的度量
1.两项资产组合的风险
两项资产组合的收益率的方差满足以下关系式：
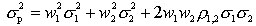
式中，σP表示资产组合的标准差，衡量资产组合的风险；σ1和 σ2分别表示组合中两项资产的标准差；W1和W2分别表示组合中两项资产所占的价值比例；P1,2反映两项资产收益率的相关程度，即两项资产收益率之间相对运动的状态，称为相关系数。理论上，相关系数处于区间［一1，1］内。
当P1,2=1时，表明两项资产的收益率具有完全正相关的关系，即它们的收益率变化方向和变化幅度完全相同，这时σ2P=（W1σ1+W2σ2）2，即σ2P达到最大。由此表明，组合的风险等于组合中各项资产风险的加权平均值。换句话说，当两项资产的收益率完全正相关时，两项资产的风险完全不能互相抵消，所以这样的资产组合不能降低任何风险。
当P1,2=—1时，表明两项资产的收益率具有完全负相关的关系，即它们的收益率变化方向和变化幅度完全相反。这时σ2P=（W1σ1—W2σ2）2，即σ2P达到最小，甚至可能是零。因此，当两项资产的收益率具有完全负相关关系时，两者之间的风险可以充分地相互抵消，甚至完全消除。因而，由这样的资产组成的组合就可以最大程度地抵消风险。
在实际中，两项资产的收益率具有完全正相关或完全负相关关系的情况几乎是不可能的。绝大多数资产两两之间都具有不完全的相关关系，即相关系数小于1 且大于一1 （多数情况下大于零）。因此，会有0<σP<（W1σ1+W2σ2），即资产组合的标准差小于组合中各资产标准差的加权平均，也即资产组合的风险小于组合中各资产风险之加权平均值，因此资产组合才可以分散风险。资产组合所分散掉的是由方差表示的各资产本身的风险，而由协方差表示的各资产收益率之间相互作用、共同运动所产生的风险，是不能通过资产组合来消除的。
2.多项资产组合的风险
一般来讲，由于每两项资产间具有不完全的相关关系，因此随着资产组合中资产个数的增加，资产组合的风险会逐渐降低。但当资产的个数增加到一定程度时，资产组合的风险程度将趋于平稳，这时资产组合风险的降低将非常缓慢直至不再降低。
那些只反映资产本身特性，由方差表示的各资产本身的风险，会随着组合中资产个数的增加而逐渐减小，当组合中资产的个数足够大时，这部分风险可以被完全消除。我们将这些可通过增加组合中资产的数目而最终消除的风险称为非系统风险。
而那些由协方差表示的各资产收益率之间相互作用、共同运动所产生的风险，并不能随着组合中资产数目的增加而消失，它是始终存在的。这些无法最终消除的风险被称为系统风险。
二、非系统风险与风险分散
非系统风险，又被称为企业特有风险或可分散风险，是指由于某种特定原因对某特定资产收益率造成影响的可能性。它是可以通过有效的资产组合来消除掉的风险；它是特定企业或特定行业所特有的，与政治、经济和其他影响所有资产的市场因素无关。对于特定企业而言，企业特有风险可进一步分为经营风险和财务风险。经营风险，是指因生产经营方面的原因给企业目标带来不利影响的可能性。财务风险，又称筹资风险，是指由于举债而给企业目标带来不利影响的可能性。
在风险分散的过程中，不应当过分夸大资产多样性和资产数目的作用。实际上，在资产组合中资产数目较少时，通过增加资产的数目，分散风险的效应会比较明显，但当资产的数目增加到一定程度时，风险分散的效应就会逐渐减弱。
三、系统风险及其衡量
系统风险，又被称为市场风险或不可分散风险，是影响所有资产的、不能通过资产组合来消除的风险。这部分风险是由那些影响整个市场的风险因素所引起的。这些因素包括宏观经济形势的变动、国家经济政策的变化、税制改革、企业会计准则改革、世界能源状况、政治因素等。
单项资产或资产组合受系统风险影响的程度，可以通过β系数来衡量。
（一）单项资产的β系数
单项资产的β系数，是指可以反映单项资产收益率与市场平均收益率之间变动关系的一个量化指标。它表示单项资产收益率的变动受市场平均收益率变动的影响程度。换句话说，就是相对于市场组合的平均风险而言，单项资产系统风险的大小。
β系数的定义式如下：
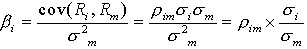
式中，Pim表示第i项资产的收益率与市场组合收益率的相关系数；σi是第i项资产收益率的标准差，表示该资产的风险大小；σm是市场组合收益率的标准差，表示市场组合的风险；σim 、σi 和 σm三个指标的乘积表示第i项资产收益率与市场组合收益率的协方差。
（二）市场组合及其风险的概念
市场组合，是指由市场上所有资产组成的组合。它的收益率就是市场平均收益率，实务中通常用股票价格指数的收益率来代替。而市场组合的方差则代表了市场整体的风险。由于包含了所有的资产，因此市场组合中的非系统风险已经被消除，所以市场组合的风险就是市场风险。
当某资产的β系数等于1 时，说明该资产的收益率与市场平均收益率呈同方向、同比例的变化，即如果市场平均收益率增加（或减少）1 % ，那么该资产的收益率也相应的增加（或减少）1 % ，也就是说，该资产的系统风险与市场组合的风险一致；当某资产的β系数小于1 时，说明该资产收益率的变动幅度小于市场组合收益率的变动幅度，因此其系统风险小于市场组合的风险；当某资产的β系数大于1 时，说明该资产收益率的变动幅度大于市场组合收益率的变动幅度，因此其系统风险大于市场组合的风险。
绝大多数资产的β系数是大于零的，即绝大多数资产收益率的变化方向与市场平均收益率的变化方向是一致的，只是变化幅度不同而导致β系数的不同；极个别资产的β系数是负数，表明这类资产的收益率与市场平均收益率的变化方向相反，当市场的平均收益增加时，这类资产的收益却在减少。
（三）资产组合的β系数
对于资产组合来说，其系统风险的大小也可以用β系数来衡量。资产组合的β系数是所有单项资产β系数的加权平均数，权数为各种资产在资产组合中所占的价值比例。其计算公式为：
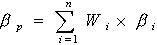
式中，βp是资产组合的 系数；Wi为第i项资产在组合中所占的价值比重；βi表示第i项资产的β系数。
由于单项资产的β系数不尽相同，因此通过替换资产组合中的资产或改变不同资产在组合中的价值比例，可以改变资产组合的风险特性。
第三节 证券市场理论
在市场机制的作用下，证券市场自发地对各种证券的风险与收益进行报考调整最终实现风险和收益的均衡状态，并由此产生了证券市场理论。
一、风险与收益的一般关系
对于每项资产，投资者都会因承担风险而要求获得额外的补偿，其要求的最低收益率应该包括无风险收益率与风险收益率两部分。因此，对于每项资产来说，所要求的必要收益率可以用以下的模式来度量：
必要收益率＝无风险收益率＋风险收益率
式中，无风险收益率（通常用Rf表示）是纯利率与通货膨胀补贴率之和，通常用短期国债的收益率来近似的替代；风险收益率则表示因承担该项资产的风险而要求获得的额外补偿，其大小则视所承担风险的大小以及投资者对风险的偏好而定。
风险收益率可以表述为风险价值系数（b）与标准离差率（V）的乘积。即：
风险收益率＝b×V
因此
必要收益率（R） = Rf+b×V
风险价值系数的大小取决于投资者对风险的偏好，对风险的态度越是回避，风险价值系数的值也就越大；反之则越小。标准离差率的大小则由该项资产的风险大小所决定。
二、资本资产定价模型
（一）资本资产定价模型（CAPM）
1.资本资产定价模型的基本原理
资本资产定价模型的主要内容是分析风险收益率的决定因素和度量方法，其核心关系式为：
R＝Rf＋β×（Rm一Rf）
式中，R表示某资产的必要收益率；β表示该资产的系统风险系数；Rf表示无风险收益率，通常以短期国债的利率来近似的替代；Rm表示市场平均收益率，通常用股票价格指数来代替。
公式中的（Rm一Rf）称为市场风险溢酬，它是附加在无风险收益率之上的，由于承担了市场平均风险所要求获得的补偿，它反映的是市场作为整体对风险的平均“容忍”程度。对风险的平均容忍程度越低，越厌恶风险，要求的收益率就越高，市场风险溢酬就越大；反之，市场风险溢酬则越小。
某项资产的风险收益率是市场风险溢酬与该资产的β系数的乘积。即：
风险收益率＝β×（Rm一Rf）
2.证券市场线（SML）
如果把资本资产定价模型核心关系式中的系统风险系数（β）看作自变量，必要收益率（R）作为因变量，无风险利率（Rf）和市场风险溢酬（Rm一Rf）作为已知系数，那么这个关系式在数学上就是一个直线方程，叫做证券市场线。即关系式R＝Rf＋β×（Rm一Rf）所代表的直线。该直线的横坐标是β系数，纵坐标是必要收益率。
证券市场线上每个点的横、纵坐标分别对应着每一项资产（或资产组合）的系统风险系数和必要收益率。因此，证券市场上任意一项资产或资产组合的系统风险系数和必要收益率都可以在证券市场线上找到对应的一点。
3.资产组合的必要收益率
资产组合的必要收益率也可用证券市场线来描述：
资产组合的必要收益率=Rf＋βp×（Rm一Rf）
式中，βp是资产组合的系统风险系数。
