1.证券市场线对证券市场的描述
市场风险溢酬(Rm一Rf)反映的是市场整体对风险的偏好,如果风险厌恶程度高,则市场风险溢酬的值就大,那么当某项资产的系统风险水平(用β表示)稍有变化时,就会导致该项资产的必要收益率以较大幅度变化;相反,如果多数市场参与者对风险的关注程度较小,那么资产的必要收益率受其系统风险的影响则较小。
当无风险收益率上涨而其他条件不变时,所有资产的必要收益率都会上涨同样的数量;反之,当无风险收益率下降且其他条件不变时,所有资产的必要收益率都会下降同样的数量。
2.证券市场线与市场均衡
资本资产定价模型认为,证券市场线是一条市场均衡线,市场在均衡的状态下,所有资产的预期收益都应该落在这条线上。也就是说,在均衡状态下,每项资产的预期收益率应该等于其必要收益率,其大小由证券市场线的核心公式来决定。
在资本资产定价模型的理论框架下,假设市场是均衡的,则资本资产定价模型还可以描述为:
预期收益率=必要收益率=Rf+β×(Rm一Rf)
3.资本资产定价模型的有效性和局限性
资本资产定价模型和证券市场线最大的贡献在于它描述了风险与收益之间的数量关系,首次将“高收益伴随着高风险”的直观认识,用简单的关系式表达出来。
但在实际运用中,该模型仍存在着一些明显的局限,主要表现在:(1)某些资产或企业的β值难以估计,对于那些缺乏历史数据的新兴行业而言尤其如此;(2 ) 即使有充足的历史数据可以利用,但由于经济环境的不确定性和不断变化,使得依据历史数据估算出来的β值对未来的指导作用大打折扣;(3)资本资产定价模型和证券市场线是建立在一系列假设之上的,其中一些假设与实际情况有较大的偏差。
三、套利定价理论
套利定价理论(APT ) ,也是讨论资产的收益率如何受风险因素影响的理论。所不同的是,套利定价理论认为资产的预期收益率并不是只受单一风险的影响,而是受若干个相互独立的风险因素,如通货膨胀率、利率、石油价格、国民经济的增长指标等的影响,是一个多因素的模型。
该模型的基本形式为:
E(R)=Rf*+b1λ1+b2λ2+…+bnλn
式中,E(R)表示某项资产的预期收益率;Rf*表示不包括通货膨胀因素的无风险收益率,即纯利率;bi表示风险因素i对该资产的影响程度,称为资产对风险因素i 的响应系数;λi表示风险因素i的预期收益率,即该资产由于承担风险因素i而预期获得的收益率。
[ 基本要求]
(一)掌握复利现值和终值的含义与计算方法
(二)掌握年金现值、年金终值的含义与计算方法
(三)掌握利率的计算,名义利率与实际利率的换算
(四)掌握股票收益率的计算,普通股的评价模型
(五)掌握债券收益率的计算,债券的估价模型
(六)熟悉现值系数、终值系数在计算资金时间价值中的运用
(七)熟悉股票和股票价格
(八)熟悉债券的含义和基本要素
[考试内容]
第一节 资金时间价值
一、资金时间价值的含义
资金时间价值,是指一定量资金在不同时点上的价值量差额。资金的时间价值来源于资金进入社会再生产过程后的价值增值。通常情况下,它相当于没有风险也没有通货膨胀情况下的社会平均利润率,是利润平均化规律发生作用的结果。
根据资金具有时间价值的理论,可以将某一时点的资金金额折算为其他时点的金额。
二、现值与终值的计算
现值,是指未来某一时点上的一定量资金折算到现在所对应的金额,通常记作P0 终值又称为将来值,是现在一定量的资金折算到未来某一时点所对应的金额,通常记作F0
现值和终值概念可以适当推广。对于所分析的任意一段时间,资金在起始时刻的价值量都可以称为现值;资金在终了时刻的价值量都可以称为终值。一定量资金的终值与现值的差额即为资金的时间价值;连接现值和终值并实现两者相互折算的百分数称为折现率。现实生活中“本金”、“本利和”的说法相当于资金时间价值理论中的“现值”和“终值”概念,利息和利率类似于资金时间价值的绝对数和相对数形式,利率经常被当作折现率使用。现值和终值对应的时点之间可以划分为若干个计息周期。
(一)现值和终值的基本计算
利息的计算有单利和复利两种方式,在不同的计息方式下,现值和终值之间的数量关系不同。通常情况下,资金时间价值采用复利计息方式进行计算。
1.单利计息方式下现值与终值的关系
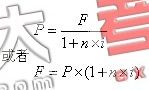

(二)年金现值和年金终值的计算
如果多期发生现金流,则每期现金流均按现值和终值的基本公式计算。多期现金流的一种特殊情况是,现金流入(或者流出)间隔的时间相同、金额相等,这种类型的系列现金流称为年金,每期流入(或流出)的金额用A表示。年金按其每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
1.普通年金的现值和终值的计算
普通年金又称后付年金,是指从第1期起,在一定时期内每期期末等额收付的系列款项。普通年金有时也简称年金。
(1)普通年金的现值计算公式与现值系数

2.即付年金现值系数和终值系数
即付年金又称先付年金,是指从第1 期起,在一定时期内每期期初等额收付的系列款项。即付年金与普通年金的区别在于,即付年金的收付行为发生在每期期初,而普通年金的收付行为发生在每期期末。
即付年金现值系数=(1+i)×普通年金现值系数
即付年金终值系数=(1+i)×普通年金终值系数
3.递延年金
如果在所分析的期间中,前m 期没有年金收付,从第m +1期开始形成普通年金,这种情况下的系列款项称为递延年金。计算递延年金的现值可以先计算普通年金现值,然后再将该现值视为终值,折算为第1期期初的现值。递延年金终值与普通年金终值的计算相同。
4.永续年金
普通年金的期数n 趋向于无穷大时形成永续年金。永续年金不计算终值。

(三)现值与终值系数表
显然,现值、终值系数的所有公式都只需要三个因素:计息方式、每期利率和期数。在复利计息方式下,由不同利率i和期数n 的组合计算出各种情况下的现值和终值系数,并依照一定顺序排列成复利现值系数表、复利终值系数表、年金现值系数表、年金终值系数表等。在计算资金的时间价值时,只需要根据i ,n 两个因素查询相应表格,即可获得有关现值系数和终值系数。
三、利率的计算
(一)复利计息方式下利率的计算
利率、现值(或者终值)系数之间存在一定的数量关系。已知现值(或者终值)
系数,则可以通过内插法公式计算出对应的利率:

1.若已知复利现值(或者终值)系数B 以及期数n可以查“复利现值(或者终值)系数表”,找出与已知复利现值(或者终值)系数最接近的两个系数及其对应的利率,按内插法公式计算出利率。
2.若已知年金现值(或者终值)系数B 以及期数几可以查“年金现值(或者终值)系数表”,找出与已知年金现值(或者终值)系数最接近的两个系数及其对应的利率,按内插法公式计算出利率。
3.永续年金的利率可以通过公式, 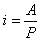 计算得出。
计算得出。
(二)名义利率与实际利率
如果以“年”作为基本计息期,每年计算一次复利,这种情况下的年利率为名义利率。如果按照短于1 年的计息期计算复利,并将全年利息额除以年初的本金,此时得到的利率则为实际利率。名义利率与实际利率的换算关系如下:
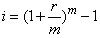
式中,i实际利率;r名义利率;m为每年复利次数。
第二节 普通股及其评价
一、股票与股票收益率
(一)股票的价值与价格
股票,是股份公司发行的、用以证明投资者的股东身份和权益,并据以获得股利的一种可转让的证明。
1.股票的价值形式
股票的价值形式有票面价值、账面价值、清算价值和市场价值。
2.股票的价格
股票价格有广义和狭义之分。狭义的股票价格就是股票交易价格;广义的股票价格则包括股票的发行价格和交易价格两种形式。股票交易价格具有事先的不确定性和市场性特点。
3.股价指数
股价指数,是指金融机构通过对股票市场上一些有代表性的公司发行的股票价格进行平均计算和报考对比后得出的数值,它是用以表示多种股票平均价格水平及其变动,并权衡股市行情的指标。股价指数的计算方法有简单算术平均法、综合平均法、几何平均法和加权综合法等。
(二)股票的收益率
股票的收益,是指投资者从购入股票开始到出售股票为止整个持有期间的收入,由股利和资本利得两方面组成。
股票收益率是股票收益额与购买成本之比。为便于与其他年度收益指标相比较,可折算为年均收益率。股票收益率主要有本期收益率、持有期收益率两种。
本期收益率,是指股份公司上年派发的现金股利与本期股票价格的比率,反映了以现行价格购买股票的预期收益情况。

式中,年现金股利是指上年发放的每股股利;本期股票价格是指该股票当日证券市场收盘价。
持有期收益率,是指投资者买入股票持有一定时期后又将其卖出,在投资者持有该股票期间的收益率,反映了股东持有股票期间的实际收益情况。
如投资者持有股票的时间不超过1 年,不考虑复利计息问题,其持有期收益率可按如下公式计算:

二、普通股的评价模型
普通股的价值(内在价值)是由普通股产生的未来现金流量的现值决定的,股票给持有者带来的未来现金流入包括两部分:股利收入和股票出售时的资本利得。股票的价值由一系列的股利和将来出售股票时进、售价的差额所构成。其基本计算公式是:
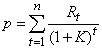
式中,P 是股票价值;Rt是股票第t年产生的现金流入量(包括股利收入、卖出股票的资本利得);K是折现率;n是持有年限。
(一)股利固定模型
如果长期持有股票,且各年股利固定,其支付过程即为一个永续年金,则该股票价值的计算公式为:
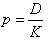
式中,D为各年收到的固定股息;其他符号的含义与基本公式相同。
(二)股利固定增长模型
从理论上看,企业的股利不应当是固定不变的,而应当是不断增长的。假定企业长期持有股票,且各年股利按照固定比例增长,则股票价值计算公式为:

(三)三阶段模型
在现实生活中,有的公司股利是不固定的。如果预计未来一段时间内股利将高速增长,接下来的时间则为正常固定增长或者固定不变,则可以分别计算高速增长、正常固定增长、固定不变等各阶段未来收益的现值,各阶段现值之和就是股利非固定增长情况下的股票价值。

(四)普通股评价模型的局限性
1.未来经济利益流入量的现值只是决定股票价值的基本因素而不是全部因素,其他很多因素(如投机行为等)可能会导致股票的市场价格大大偏离根据模型计算得出的价值。
2.模型对未来期间股利流入量预测数的依赖性很强,而这些数据很难准确预测。股利固定不变、股利固定增长等假设与现实情况可能存在一定差距。
3.股利固定模型、股利固定增长模型的计算结果受D0 或Dl 的影响很大,而这两个数据可能具有人为性、短期性和偶然性,模型放大了这些不可靠因素的影响力。
4.折现率的选择有较大的主观随意性。
第三节 债券及其评价
一、债券及其构成要素
债券,是债务人依照法定程序发行, 承诺按约定的利率和日期支付利息,并在特定日期偿还本金的书面债务凭证。
一般而言,债券包括面值、期限、利率和价格等基本要素。
二、债券的评价
(一)债券的估价模型
债券的估价是对债券在某一时点的价值量的估算,是债券评价的一项重要内容。对于新发行的债券而言,估价模型的计算结果反映了债券的发行价格。
1.债券估价的基本模型
债券估价的基本模型,是指对典型债券所使用的估价模型,典型债券是票面利率固定,每年年末计算并支付当年利息、到期偿还本金的债券。这种情况下,新发行债券的价值可采用如下模型进行评定:

式中符号的含义与债券估价的基本模型相同。
(二)债券收益的来源及影响收益率的因素
债券的收益主要包括两方面的内容:一是债券的利息收入;二是资本损益,即债券买入价与卖出价(在持有至到期的情况下为到期偿还额)之间的差额,当卖出价高于买入价时为资本收益,反之为资本损失。此外,有的债券还可能因参与公司盈余分配,或者拥有转股权而获得额外收益。
决定债券收益率的因素主要有债券票面利率、期限、面值、持有时间、购买价格和出售价格。



